 .
. Uma das coisas que pensei foi fazer
![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png) mas não sei como aplicar a informação...
mas não sei como aplicar a informação...
 .
. ![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png) mas não sei como aplicar a informação...
mas não sei como aplicar a informação...
Danilo escreveu:Determine Z pertencente ao conjunto dos números complexos tal que.
Uma das coisas que pensei foi fazermas não sei como aplicar a informação...
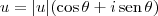 . Se z é uma raiz n-ésima de u, isto é,
. Se z é uma raiz n-ésima de u, isto é,  , então temos que:
, então temos que:![z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right] z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right]](/latexrender/pictures/635e910fd5fb7ad17249731c4f9d85a4.png) , com k = 0, 1, 2, ..., n-1.
, com k = 0, 1, 2, ..., n-1.
LuizAquino escreveu:Danilo escreveu:Determine Z pertencente ao conjunto dos números complexos tal que.
Uma das coisas que pensei foi fazermas não sei como aplicar a informação...
Eu recomendo que você estude o conteúdo "Radiciação de Números Complexos".
Considere um número complexo. Se z é uma raiz n-ésima de u, isto é,
, então temos que:
, com k = 0, 1, 2, ..., n-1.
Agora tente aplicar essa fórmula.


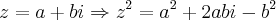
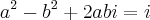
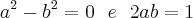
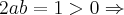
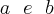 deve ter o mesmo sinal onde
deve ter o mesmo sinal onde ![a=b= \pm\frac{\sqrt[]{2}}{2} a=b= \pm\frac{\sqrt[]{2}}{2}](/latexrender/pictures/db6efe5c5d03971669b1cf87c67dcdd2.png) .
.![z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i](/latexrender/pictures/94a7f3003ada7377a3a2695e3a3dc776.png)



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)