 por Danilo » Dom Ago 26, 2012 19:59
por Danilo » Dom Ago 26, 2012 19:59
Determine Z pertencente ao conjunto dos números complexos tal que

.
Uma das coisas que pensei foi fazer
![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png)
mas não sei como aplicar a informação...
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Dom Ago 26, 2012 21:37
por LuizAquino » Dom Ago 26, 2012 21:37
Danilo escreveu:Determine Z pertencente ao conjunto dos números complexos tal que

.
Uma das coisas que pensei foi fazer
![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png)
mas não sei como aplicar a informação...
Eu recomendo que você estude o conteúdo "Radiciação de Números Complexos".
Considere um número complexo
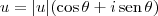
. Se z é uma raiz n-ésima de u, isto é,

, então temos que:
![z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right] z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right]](/latexrender/pictures/635e910fd5fb7ad17249731c4f9d85a4.png)
, com k = 0, 1, 2, ..., n-1.
Agora tente aplicar essa fórmula.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Qua Ago 29, 2012 10:28
por Danilo » Qua Ago 29, 2012 10:28
LuizAquino escreveu:Danilo escreveu:Determine Z pertencente ao conjunto dos números complexos tal que

.
Uma das coisas que pensei foi fazer
![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png)
mas não sei como aplicar a informação...
Eu recomendo que você estude o conteúdo "Radiciação de Números Complexos".
Considere um número complexo
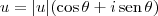
. Se z é uma raiz n-ésima de u, isto é,

, então temos que:
![z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right] z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right]](/latexrender/pictures/635e910fd5fb7ad17249731c4f9d85a4.png)
, com k = 0, 1, 2, ..., n-1.
Agora tente aplicar essa fórmula.
Beleza!

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vmo_apora » Sex Set 21, 2012 19:45
por vmo_apora » Sex Set 21, 2012 19:45
Será que está não seria uma solução interessante:
Seja
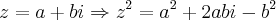
Pelo enunciado
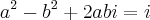
Pela igualdade dos complexos:
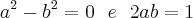
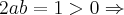
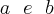
deve ter o mesmo sinal onde
![a=b= \pm\frac{\sqrt[]{2}}{2} a=b= \pm\frac{\sqrt[]{2}}{2}](/latexrender/pictures/db6efe5c5d03971669b1cf87c67dcdd2.png)
.
Então podemos ter
![z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i](/latexrender/pictures/94a7f3003ada7377a3a2695e3a3dc776.png)
-
vmo_apora
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 13, 2011 16:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por MarceloFantini » Sex Set 21, 2012 23:53
por MarceloFantini » Sex Set 21, 2012 23:53
Perfeitamente válida, mas pode ser muito trabalhosa para um caso genérico. Resolver esse sistema pode gerar uma dor de cabeça grande, enquanto que pela notação de Euler tudo é resolvido de modo simples.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números complexos] Dúvida
por iceman » Qui Mai 10, 2012 18:52
- 5 Respostas
- 3744 Exibições
- Última mensagem por fraol

Qui Mai 10, 2012 21:15
Números Complexos
-
- Números Complexos - Dúvida
por iceman » Ter Mai 15, 2012 20:22
- 1 Respostas
- 1809 Exibições
- Última mensagem por fraol

Ter Mai 15, 2012 22:20
Números Complexos
-
- Dúvida - Números complexos
por Danilo » Sex Ago 03, 2012 02:05
- 5 Respostas
- 3845 Exibições
- Última mensagem por Danilo

Sex Ago 03, 2012 16:46
Números Complexos
-
- Dúvida - números complexos
por Danilo » Ter Ago 07, 2012 14:51
- 4 Respostas
- 3126 Exibições
- Última mensagem por LuizAquino

Qua Ago 08, 2012 11:38
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17106 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
. ![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png) mas não sei como aplicar a informação...
mas não sei como aplicar a informação...
 .
. ![z = \sqrt[]{i} z = \sqrt[]{i}](/latexrender/pictures/2ed636678063b3f50530c8d961b2ca50.png) mas não sei como aplicar a informação...
mas não sei como aplicar a informação...
.
mas não sei como aplicar a informação...
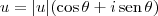 . Se z é uma raiz n-ésima de u, isto é,
. Se z é uma raiz n-ésima de u, isto é,  , então temos que:
, então temos que:![z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right] z = \sqrt[n]{|u|}\left[\cos\left(\frac{\theta+2k\pi}{n}\right) + i\,\textrm{sen}\,\left(\frac{\theta+2k\pi}{n}\right)\right]](/latexrender/pictures/635e910fd5fb7ad17249731c4f9d85a4.png) , com k = 0, 1, 2, ..., n-1.
, com k = 0, 1, 2, ..., n-1.
.
mas não sei como aplicar a informação...
. Se z é uma raiz n-ésima de u, isto é,
, então temos que:
, com k = 0, 1, 2, ..., n-1.


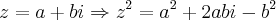
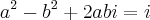
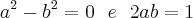
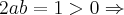
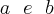 deve ter o mesmo sinal onde
deve ter o mesmo sinal onde ![a=b= \pm\frac{\sqrt[]{2}}{2} a=b= \pm\frac{\sqrt[]{2}}{2}](/latexrender/pictures/db6efe5c5d03971669b1cf87c67dcdd2.png) .
.![z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i z=\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}i~~ou~~z=-\frac{\sqrt[]{2}}{2}-\frac{\sqrt[]{2}}{2}i](/latexrender/pictures/94a7f3003ada7377a3a2695e3a3dc776.png)





 , avisa que eu resolvo.
, avisa que eu resolvo.

