Jhenrique escreveu:Claro! Então... minha dúvida surgiu quando eu assisti a video aula 17 do Luiz Aquino, "Aproximação Linear e Diferencial". Nela, como na anterior ("Derivada de Ordem Superior"), ele manipula os diferenciais x e y normalmente, como se fossem variáveis quaisquer, e eu achei isso muitíssimo estranho, porque na video aula 13 dele, Regra da Cadeia, ele enfatiza claramente que não podemos simplificar um diferencial de um denominador com um diferencial do numerador seguinte. Mas como eu disse, em aulas futuras, ele os manipula normalmente, e isso eu não entendi muito bem... outra coisa também que não ficou muito claro é pq no exemplo 2 da video aula 17, o valor do dy é diferente do valor do ?y. Ele derivou a expressão do exemplo e calculou o valor de dy usando os mesmos dados do problema usados para calcular o valor de ?y, os valores são diferentes, não entendi porque... o que eu cheguei mais próximo de entender foi uma parte da resposta particular dele para mim que eu postei abrindo este tópico.
O Luiz me afirmou que o dy é da reta tangente "r", enquanto que o ?y é duma função qualquer "f"... rapidamente eu pensei que na aproximação diferencial, o dy pode ser diferente de ?y por essa razão, mas na definição de derivada imaginei que dy e ?y são idênticos.
Para que os outros participantes do fórum saibam de que aulas você está falando, você se refere as videoaulas do curso de Cálculo I que estão disponíveis no meu canal:
http://www.youtube.com/LCMAquinoEm relação a sua dúvida, você está confundindo a notação de Leibniz "dy/dx", que serve para representar a derivada de uma função, com um quociente "dy/dx" que usamos em aproximação diferencial. Na notação de Leibniz, não estamos enxergando dy/dx como uma "mera" divisão entre os números dy e dx. Na verdade, dy/dx representa um limite nessa notação. Já na aproximação diferencial queremos dar um significado para a divisão entre os números dy e dx. Ou seja, um significado para dy/dx que não seja simplesmente uma notação. Considere então a figura abaixo.
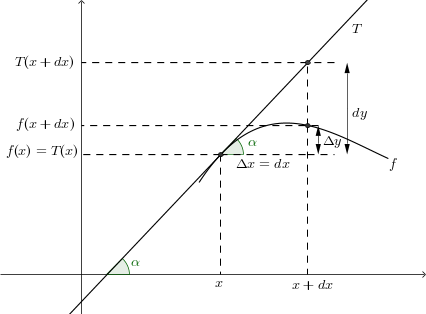
- figura.png (10.9 KiB) Exibido 3606 vezes
Suponha que T seja a reta tangente a função f no ponto (x, f(x)). Façamos as seguintes definições:
(i) vamos chamar de
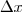
a variação da grandeza x. Por exemplo, se x variou de

até

, então
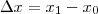
. No nosso caso, como x variou de x até x + dx, teremos que
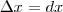
;
(ii) vamos chamar de

a variação da grandeza y (lembrando que y é uma função de x) quando houve uma variação na grandeza x. Por exemplo, se x variou de

até

, então
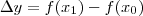
. No nosso caso, como x variou de x até x + dx, teremos que

;
(iii) vamos chamar de dy a variação da grandeza T quando houve uma variação na grandeza x. Por exemplo, se x variou de

até

, então
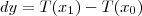
. No nosso caso, como x variou de x até x + dx, teremos que
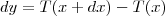
.
Analisando essas definições, perceba que teremos
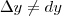
. Mas note que dy servirá como uma aproximação para

.
Considere agora o ângulo alfa, formado pela reta tangente T e o eixo x. Da definição de derivada, sabemos que

. Mas por outro lado, analisando o triângulo retângulo que tem hipotenusa em T e catetos medindo dx e dy, temos que

. Concluímos então nesse caso que
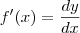
. Aqui estamos enxergando "dy/dx" como um quociente entre os números dy e dx que definimos anteriormente. Não estamos enxergando "dy/dx" como uma "mera" notação para representar a derivada de uma função. Sendo assim, como "dy/dx" é um quociente nesse caso, podemos escrever dy = f'(x)dx. Isso nos fornece uma forma de calcular dy sendo dados f'(x) e dx.
Agora faça um exemplo. Considere a função
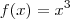
. Suponha que x variou de 5 até 5,2, ou seja, dx = 0,2. Agora calcule

e

. Compare os valores de

e dy. Faça também um esboço do gráfico de f e interprete esses dois valores.
ObservaçãoCom base em toda essa discussão, note como a notação de Leibniz é bem conveniente. A expressão "dy/dx" usada apenas como uma "mera" notação (uma "escrita"), também pode ter uma interpretação como um quociente entre os números dy e dx, desde que esses números sejam definidos de forma adequada.




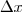 a variação da grandeza x. Por exemplo, se x variou de
a variação da grandeza x. Por exemplo, se x variou de  até
até  , então
, então 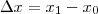 . No nosso caso, como x variou de x até x + dx, teremos que
. No nosso caso, como x variou de x até x + dx, teremos que 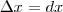 ;
; a variação da grandeza y (lembrando que y é uma função de x) quando houve uma variação na grandeza x. Por exemplo, se x variou de
a variação da grandeza y (lembrando que y é uma função de x) quando houve uma variação na grandeza x. Por exemplo, se x variou de 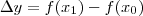 . No nosso caso, como x variou de x até x + dx, teremos que
. No nosso caso, como x variou de x até x + dx, teremos que  ;
;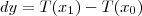 . No nosso caso, como x variou de x até x + dx, teremos que
. No nosso caso, como x variou de x até x + dx, teremos que 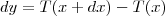 .
.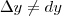 . Mas note que dy servirá como uma aproximação para
. Mas note que dy servirá como uma aproximação para  . Mas por outro lado, analisando o triângulo retângulo que tem hipotenusa em T e catetos medindo dx e dy, temos que
. Mas por outro lado, analisando o triângulo retângulo que tem hipotenusa em T e catetos medindo dx e dy, temos que  . Concluímos então nesse caso que
. Concluímos então nesse caso que 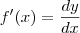 . Aqui estamos enxergando "dy/dx" como um quociente entre os números dy e dx que definimos anteriormente. Não estamos enxergando "dy/dx" como uma "mera" notação para representar a derivada de uma função. Sendo assim, como "dy/dx" é um quociente nesse caso, podemos escrever dy = f'(x)dx. Isso nos fornece uma forma de calcular dy sendo dados f'(x) e dx.
. Aqui estamos enxergando "dy/dx" como um quociente entre os números dy e dx que definimos anteriormente. Não estamos enxergando "dy/dx" como uma "mera" notação para representar a derivada de uma função. Sendo assim, como "dy/dx" é um quociente nesse caso, podemos escrever dy = f'(x)dx. Isso nos fornece uma forma de calcular dy sendo dados f'(x) e dx.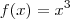 . Suponha que x variou de 5 até 5,2, ou seja, dx = 0,2. Agora calcule
. Suponha que x variou de 5 até 5,2, ou seja, dx = 0,2. Agora calcule  e
e  . Compare os valores de
. Compare os valores de