por anneliesero » Qui Set 13, 2012 18:03
por anneliesero » Qui Set 13, 2012 18:03
Olá,
Vocês podem me ajudar a resolver este exercício:
1. Em um triângulo retângulo ABC , a diferença entre os catetos é 2 cm e o produto é 48 cm² . Determine a hipotenusa desse triângulo.
*OBS.: Eu já olhei um outro tópico com uma pergunta parecida com está, mas não entendi.

''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qui Set 13, 2012 18:19
por Cleyson007 » Qui Set 13, 2012 18:19
Olá, boa tarde!
Primeiramente, seja bem-vinda ao AjudaMatemática!
Vou te dar as dicas, ok?
1° - Chame um cateto de "x" e o outro de "x + 2" (Pois um cateto é maior que o outro em 2cm).
2° - Chame a hipotenusa do triângulo retângulo de "y".
3° - Por Pitágoras, temos: y² = x² + (x + 2)²
4° - Produto dos catetos é igual a 48cm² -->
(x)(x + 2)² = 48 (Resolva e encontre o valor de x)
5° - Para encontrar y, substitua o valor que encontrou de x na equação y² = x² + (x + 2)².
Agora tente resolver!
Comente qualquer dúvida

Cleyson007
Editado pela última vez por
Cleyson007 em Sex Set 14, 2012 09:31, em um total de 2 vezes.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por anneliesero » Qui Set 13, 2012 18:37
por anneliesero » Qui Set 13, 2012 18:37
Bem, ficou assim:
(x²)(x + 2)² = 48
(x²) (x²+4)=48
x^4+4x²+4x²+4x²
12x^6=x^4
x^6= x^4/12
E depois? Como faço?
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Set 13, 2012 20:08
por young_jedi » Qui Set 13, 2012 20:08
Na realidade o produto dos catetos é dado por
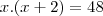
resolvendo isto voce encontra os dois catetos e depois por pitagoras a hipotenusa
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Cleyson007 » Sex Set 14, 2012 09:36
por Cleyson007 » Sex Set 14, 2012 09:36
Bom dia!
Anneliesero, desculpe pelo descuido.. Editei minha resposta "em vermelho".
Obrigado Young_Jedi por conferir!
Tente resolver agora e, caso haja dúvidas, entre em contato.

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 16:54
- 1 Respostas
- 3179 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:42
Trigonometria
-
- RE: TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 17:08
- 2 Respostas
- 6777 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:31
Trigonometria
-
- [Trigonometria no triângulo retângulo]
 por Victor985 » Ter Nov 19, 2013 08:38
por Victor985 » Ter Nov 19, 2013 08:38
- 2 Respostas
- 3878 Exibições
- Última mensagem por Pessoa Estranha

Ter Nov 19, 2013 17:29
Trigonometria
-
- [Trigonometria] triângulo retângulo e isocéles
por JoseEduardo » Dom Out 09, 2011 03:25
- 2 Respostas
- 1741 Exibições
- Última mensagem por JoseEduardo

Sex Nov 04, 2011 00:44
Trigonometria
-
- [Problema]Trigonometria no Triângulo Retângulo
por ALPC » Ter Jun 18, 2013 17:31
- 0 Respostas
- 1030 Exibições
- Última mensagem por ALPC

Ter Jun 18, 2013 17:31
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.