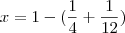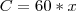Fração

[ana celia]

1-Em uma loja, o metro de corda é vendido por R$ 3,00 , e o rolo com 60 metros de corda,por R$ 150,00.Três amigos compraram juntos um rolo de corda,ficando o primeiro com 1/4 do rolo , o segundo com 1/12 e o terceiro com o restante. Se a divisão dos gastos foi proporcional à quantidade de corda que cada um recebeu , aquele que comprou a maior quantidade de corda economizou, em relação à compra da mesma quantidade de corda por metro, o total de:
resposta R$ 20,00.

1- O primeiro 1/4 -4/4 = 3/4
2- o segundo 1/12-3/4= 8/12
3-o terceiro ?restante??
Meu raciocinio está coerente? mas não consigo continuar....
Ana Célia

[young_jedi]

primerio voce deve calcular que fração o terceiro amigo ficou, isto é dado pela soma total menos a fração dos dois outros amigos ou seja:



Depois voce tem que calcular quanto ele recebeu de corda e quanto ele gastou gastou





Depois vc calcula quanto ele gastaria se comprasse essa mesma quantidade por metro (sendo 3 reais o metro) e subtraindo os gasto vc encontra o valor economizado

[Cleyson007]

Bom dia Ana!

Primeira, seja bem-vinda ao AjudaMatemática!

Sejam, " x, y e z " os compradores.

Para "x", temos: --> 1/4 (60) = 15m
Para "y", temos: --> 1/12 (60) = 5m
Para "z", temos: --> 40m (Restante para fechar os 60m) --> Pagou por metro de corda: 150/60 = R$2,50

Análise do gasto de "z" --> 2,50(40) = R$100,00
Se "z" tivesse comprado separado, teríamos: 3(40) = R$ 120,00

Logo, "z" economizou: R$ 120,00 - R$ 100,00 = R$ 20,00

Comente qualquer dúvida

Abraço,

Cleyson007

[ana celia]

Obrigada pela ajuda, vou prestar o concurso de escrevente e preciso da ajuda de vcs!!!!!!
bj