Integral dupla (Polares)

por **rubenesantos** » Dom Set 09, 2012 14:51

Olá pessoal, será que alguém pode me ajudar nessa questão? Ela deve ser respondida como polar.

Calcule:

$f(x)=\int_{0}^{4}\int_{0}^{\sqrt[]{4y-y^2}}\left(x^2+y^2\right)dxdy$

Primeiro desenhei o gráfico da função da variação de dx, confesso que precisei o Winplot. Ficou assim:
https://skydrive.live.com/?cid=f16f3547e5e4a792#cid=F16F3547E5E4A792&id=F16F3547E5E4A792%21651

A partir daí montei a seguinte integral:

$f(x)=\int_{0}^{\pi}\int_{0}^{4sen\theta} r^3drd\theta$

Resolvi a primeira integral e fiquei com o seguinte:

$f(x)=\int_{0}^{\pi}\frac{64sen^4(\theta)}{4}d\theta = 16\int_{0}^{\pi}sen^4(\theta)d\theta$

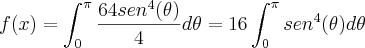
Resolvi várias vezes essa integral, através de relações trigonométricas e chegando até:

$I = 16\left[\theta-sen(2\theta) + \frac{\theta}{2} + \frac{sen(4\theta)}{8} \right]$ <<< variando de 0 até pi.

Não importa quantas vezes eu faça, chego em 24pi. Mas no gabarito da lista o resultado é 12pi.

Alguém poderia me ajudar nessa questão? Só posso pensar que estou interpretando o gráfico erroneamente.
Será que a variação de teta está errada - 0 a pi? Não vejo porque ser diferente.
Enfim, se alguém puder ajudar ficarei muito grato.

por **young_jedi** » Dom Set 09, 2012 16:49

Quando voce faz a substituição de coordenadas cartesianas para polares voce diz que

$x=rsen\theta$
$y-2=rcos\theta$

assim a integral ficaria

$\int_{0}^{\pi}\int_{0}^{2}(r^2+4rcos\theta+4)rdrd\theta$

No grafico da variação de x que vc plotou ele mostra um circulo mais na verdade a integral é so em metade do circulo

por **MarceloFantini** » Dom Set 09, 2012 17:23

Não seria $x = r \cos \theta$ e $y-2 = r \sin \theta$ ? É a substituição usual. Existe alguma razão para trocar seno e cosseno? Da forma como parametrizou o ângulo $\theta$ ele começa em $\frac{\pi}{2}$ .

por **young_jedi** » Dom Set 09, 2012 17:32

na mudança de coordenada cartesiana para polar pode ser da maneira como vc colocou tambem so que ai na integração
mudaria os limites em vez de se de 0 a $\pi$ seria de $-\frac{\pi}{2}$ a $\frac{\pi}{2}$

: area de integração; integral polar.jpg (8.94 KiB) Exibido 5018 vezes

por **rubenesantos** » Dom Set 09, 2012 19:00

Poxa, valeu mesmo. Ainda não cheguei na resposta não mas vou tentar chegar hoje.

Entendi como a função foi mudar (apesar de ainda ter dúvida na parte do $y-2=rcos\theta$ ), mas não consegui relacionar os limites de integração com o gráfico.
Pq a integral dr fica de 0 a 2? Eu não devo considerar r partindo da própria origem? (r = $4sen\theta$ )?

E, se ela fica de 0 a 2, porque d $\theta$ continua de 0 a pi e não de 0 a 2pi?

por **MarceloFantini** » Dom Set 09, 2012 19:06

O que está acontecendo é que você está integrando sob uma semi-circunferência, onde a origem está em (0,2)

e o eixo perpendicular é o eixo

.

por **rubenesantos** » Dom Set 09, 2012 19:30

young_jedi e MarceloFantini,

Meus agradecimentos. Consegui resolver agora. Foi como você falou por último Marcelo, minha falta atenção não me permitiu perceber que se tratava de uma semi-circunferência. Com sua ajuda e de Young coloquei os limites em pi/2 a -pi/2 daí ficou beleza e não precisei mudar a relação.

Valeu! =D

por **rubenesantos** » Dom Set 09, 2012 19:40

Só um detalhe, da forma que eu montei a integral no meu primeiro post, eu mudei (depois das dicas e de achar a resposta pelo outro método) os limites de integração de $d\theta$ "0 a pi" e coloquei de "0 a pi/2" e também achei 12pi. Foi pura sorte ou também pode ser feito desse jeito? Deixando a origem no mesmo lugar e fazendo r variar conforme a função $4sen\theta$ ??

De qualquer forma já consegui resolver, mais uma vez obrigado.

por **young_jedi** » Seg Set 10, 2012 10:07

Da maneira que voce postou tambem daria certo sim. A diferença esta mesmo na origem do sistema, em um metodo
se coloca a origem do sistema de coordenadas polares no ponto (0,2) do plano em coordenadas cartesianas e no seu poste inicial, está na origem (0,0).