Uma matriz A é de ordem 2, inversível, e A²=2A. Det A=?
Fiz det (2A)= det A * 2²= 4det A
Então 4det A= det A * det A
Passando det A pro outro lado 4= detA, está correto? Em uma resolução que vi na net encontrei: 2².det(A) = det(A).det(A)
4.det(A) – [det(A)]2 = 0
Não entendi por que det(A) . det(A) virou [det(A)]2


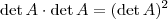 . Não sei o que você quer dizer com passar para o outro lado, mas sua solução está parcialmente correto. Se este "passar" for dividir, você está excluindo o caso em que
. Não sei o que você quer dizer com passar para o outro lado, mas sua solução está parcialmente correto. Se este "passar" for dividir, você está excluindo o caso em que 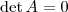 , que certamente satisfaz a equação.
, que certamente satisfaz a equação.

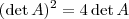 , daí
, daí 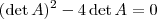 . Ponha
. Ponha  em evidência e temos
em evidência e temos 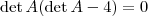 . Um produto nos números reais é zero quando pelo menos um dos seus fatores é zero, então
. Um produto nos números reais é zero quando pelo menos um dos seus fatores é zero, então  e
e  . São as duas possibilidades.
. São as duas possibilidades.![$\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$](/latexrender/pictures/16acf4c9b46f05e4b07821166d7aa361.png) então
então ![{A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ {A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/82377d99d9fc9969e9051b8947b5b98e.png) , temos também que
, temos também que  . Desta forma
. Desta forma ![$\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/1845b00cd9e06bb5cd0f5cc02093c307.png) , daí vem
, daí vem  e que
e que 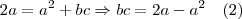
![$\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3) $\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3)](/latexrender/pictures/b56bc7da159316598e62fe787daaf6e1.png) , substituindo
, substituindo 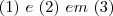 , obtemos:
, obtemos: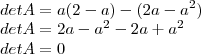

 , pois, por hipótese, a matriz
, pois, por hipótese, a matriz  é inversível, logo
é inversível, logo  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)