 por Malorientado » Sáb Set 08, 2012 14:37
por Malorientado » Sáb Set 08, 2012 14:37
Uma matriz A é de ordem 2, inversível, e A²=2A. Det A=?
Fiz det (2A)= det A * 2²= 4det A
Então 4det A= det A * det A
Passando det A pro outro lado 4= detA, está correto? Em uma resolução que vi na net encontrei: 2².det(A) = det(A).det(A)
4.det(A) – [det(A)]2 = 0
Não entendi por que det(A) . det(A) virou [det(A)]2
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Set 08, 2012 15:36
por MarceloFantini » Sáb Set 08, 2012 15:36
Porque determinante é um número, daí
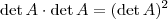
. Não sei o que você quer dizer com passar para o outro lado, mas sua solução está parcialmente correto. Se este "passar" for dividir, você está excluindo o caso em que
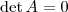
, que certamente satisfaz a equação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Malorientado » Sáb Set 08, 2012 16:38
por Malorientado » Sáb Set 08, 2012 16:38
Hum esse 2 em [det(A)]2 é expoente, não tinha visto assim. Está realmente desse jeito onde peguei a resposta. Do modo que calculei, cheguei a somente 4 mas agora que você falou vejo que 0 também é solução. Como eu deveria resolver esse exercício pra achar todas as respostas possíveis? Perdoe mas estou tendo dificuldades nessa matéria.
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Set 08, 2012 16:44
por MarceloFantini » Sáb Set 08, 2012 16:44
Deveria resolver assim: você encontrou que
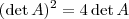
, daí
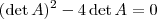
. Ponha

em evidência e temos
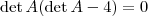
. Um produto nos números reais é zero quando pelo menos um dos seus fatores é zero, então
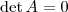
ou

e

. São as duas possibilidades.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vmo_apora » Dom Set 09, 2012 13:23
por vmo_apora » Dom Set 09, 2012 13:23
Uma outra solução poderia ser:
Seja
![$\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$](/latexrender/pictures/16acf4c9b46f05e4b07821166d7aa361.png)
então
![{A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ {A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/82377d99d9fc9969e9051b8947b5b98e.png)
, temos também que

. Desta forma
![$\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/1845b00cd9e06bb5cd0f5cc02093c307.png)
, daí vem

e que
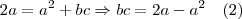
Sabe-se também que
![$\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3) $\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3)](/latexrender/pictures/b56bc7da159316598e62fe787daaf6e1.png)
, substituindo
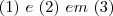
, obtemos:
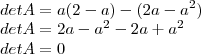
-
vmo_apora
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 13, 2011 16:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por MarceloFantini » Dom Set 09, 2012 15:06
por MarceloFantini » Dom Set 09, 2012 15:06
E o caso em que

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vmo_apora » Dom Set 09, 2012 16:23
por vmo_apora » Dom Set 09, 2012 16:23
Na verdade, a única resposta válida é

, pois, por hipótese, a matriz

é inversível, logo

.
-
vmo_apora
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 13, 2011 16:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Está correta a resolução?
por Fabio Wanderley » Qui Nov 29, 2012 11:47
- 4 Respostas
- 3771 Exibições
- Última mensagem por Fabio Wanderley

Sex Nov 30, 2012 09:36
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito] a resolução está correta?
por Fabio Wanderley » Dom Abr 01, 2012 03:20
- 2 Respostas
- 1921 Exibições
- Última mensagem por Fabio Wanderley

Dom Abr 01, 2012 15:31
Cálculo: Limites, Derivadas e Integrais
-
- Será que está correta a resolução e o resultado
por Douglas16 » Dom Mar 10, 2013 16:55
- 3 Respostas
- 4714 Exibições
- Última mensagem por Douglas16

Dom Mar 10, 2013 23:37
Cálculo: Limites, Derivadas e Integrais
-
- [Valor Desconhecido em Uma Sentença] Qual Resolução Correta?
por ShadowOnLine » Qua Ago 23, 2017 22:09
- 1 Respostas
- 3873 Exibições
- Última mensagem por DanielFerreira

Sex Ago 25, 2017 22:50
Álgebra Elementar
-
- Esta minha resolucao está correta?
por SsEstevesS » Dom Nov 27, 2011 10:29
- 0 Respostas
- 2966 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:29
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


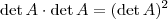 . Não sei o que você quer dizer com passar para o outro lado, mas sua solução está parcialmente correto. Se este "passar" for dividir, você está excluindo o caso em que
. Não sei o que você quer dizer com passar para o outro lado, mas sua solução está parcialmente correto. Se este "passar" for dividir, você está excluindo o caso em que 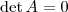 , que certamente satisfaz a equação.
, que certamente satisfaz a equação.

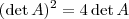 , daí
, daí 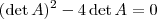 . Ponha
. Ponha  em evidência e temos
em evidência e temos 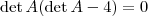 . Um produto nos números reais é zero quando pelo menos um dos seus fatores é zero, então
. Um produto nos números reais é zero quando pelo menos um dos seus fatores é zero, então  e
e  . São as duas possibilidades.
. São as duas possibilidades.![$\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
{\bf A}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$](/latexrender/pictures/16acf4c9b46f05e4b07821166d7aa361.png) então
então ![{A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ {A}^{2}=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/82377d99d9fc9969e9051b8947b5b98e.png) , temos também que
, temos também que  . Desta forma
. Desta forma ![$\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$ $\begin{array}{clcr}
\left[\begin{array}{clcr}
2a & 2b \\
2c & 2d
\end{array}\right]
\end{array}$
=
$\begin{array}{clcr}
{\bf}\left[\begin{array}{clcr}
{a}^{2} & ab + bd \\
ac + dc & bc +{d}^{2}
\end{array}\right]
\end{array}$](/latexrender/pictures/1845b00cd9e06bb5cd0f5cc02093c307.png) , daí vem
, daí vem  e que
e que 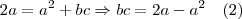
![$\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3) $\begin{array}{clcr}
{\bf detA}=\left[\begin{array}{clcr}
a & b \\
c & d
\end{array}\right]
\end{array}$
=
ad-bc~~~(3)](/latexrender/pictures/b56bc7da159316598e62fe787daaf6e1.png) , substituindo
, substituindo 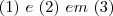 , obtemos:
, obtemos: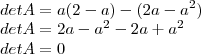

 , pois, por hipótese, a matriz
, pois, por hipótese, a matriz  é inversível, logo
é inversível, logo  .
.