 por dina ribeiro » Qua Set 05, 2012 17:40
por dina ribeiro » Qua Set 05, 2012 17:40
Boa tarde!
Estou tentando achar o módulo da deriravada da equação, mas minha resposta está diferente do "solution" do livro do Stewart

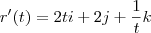
![\left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}} \left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}}](/latexrender/pictures/2da6b855ad8031e9670ea02880a649f2.png)
A resposta não seria
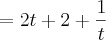
?????
Porque a resposta é

????? Porque a raíz de 4 some?
Obrigada!!!
-
dina ribeiro
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 15, 2012 19:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Qua Set 05, 2012 19:08
por Russman » Qua Set 05, 2012 19:08
Se um vetor

tem componentes
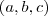
, isto é,

, então seu módulo é a quantidade
![\sqrt[]{a^2+b^2+c^2} \sqrt[]{a^2+b^2+c^2}](/latexrender/pictures/3501e3d258feb7cf848e5785ba6ae724.png)
.
Você deve selecionar as componentes uma a uma e elevá-las ao quadrado. Depois some-as e calcule a raíz quadrada positiva.
Veja que?
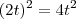

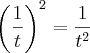
Assim, o módulo da derivada de
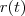
será
![\sqrt[]{4t^2 + 4 + \left(\frac{1}{t^2} \right)}=\sqrt[]{\frac{4t^4+4t^2+1}{t^2}} = \frac{1}{t}\sqrt[]{(2t^2 + 1)^2}=\frac{1}{t}\left(2t^2+1 \right) \sqrt[]{4t^2 + 4 + \left(\frac{1}{t^2} \right)}=\sqrt[]{\frac{4t^4+4t^2+1}{t^2}} = \frac{1}{t}\sqrt[]{(2t^2 + 1)^2}=\frac{1}{t}\left(2t^2+1 \right)](/latexrender/pictures/3b4e3c38295f76e0a14c0b034473e184.png)
.
Confere com o gabarito.
Note que
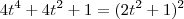
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizAquino » Qua Set 05, 2012 19:20
por LuizAquino » Qua Set 05, 2012 19:20
dina ribeiro escreveu:Estou tentando achar o módulo da deriravada da equação, mas minha resposta está diferente do "solution" do livro do Stewart

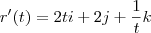
![\left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}} \left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}}](/latexrender/pictures/2da6b855ad8031e9670ea02880a649f2.png)
A resposta não seria
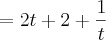
?????
Na sua resposta você cometeu um erro: achar que
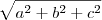
é o mesmo que a + b + c. Isso é falso! Veja um exemplo.
De um lado, temos que:

E por outro lado, temos que:
1 + 2 + 4 = 7
Note então que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5113 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
-
- Derivada e módulo
por Ana Luiza Orique » Qua Nov 23, 2016 11:10
- 0 Respostas
- 3493 Exibições
- Última mensagem por Ana Luiza Orique

Qua Nov 23, 2016 11:10
Cálculo: Limites, Derivadas e Integrais
-
- Módulo
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
- 4 Respostas
- 3013 Exibições
- Última mensagem por MarceloFantini

Sex Mar 05, 2010 16:09
Funções
-
- Modulo
por Sandy26 » Ter Abr 27, 2010 14:46
- 5 Respostas
- 3001 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Álgebra Elementar
-
- Módulo
por Bebel » Dom Ago 08, 2010 00:24
- 0 Respostas
- 1380 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:24
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

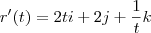
![\left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}} \left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}}](/latexrender/pictures/2da6b855ad8031e9670ea02880a649f2.png)
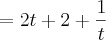 ?????
????? ????? Porque a raíz de 4 some?
????? Porque a raíz de 4 some?

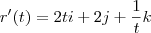
![\left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}} \left|r'(t) \right|=\sqrt[]{{4t}^{2}+4+\frac{1}{{t}^{2}}}](/latexrender/pictures/2da6b855ad8031e9670ea02880a649f2.png)
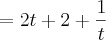 ?????
????? ????? Porque a raíz de 4 some?
????? Porque a raíz de 4 some?
 tem componentes
tem componentes 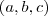 , isto é,
, isto é,  , então seu módulo é a quantidade
, então seu módulo é a quantidade ![\sqrt[]{a^2+b^2+c^2} \sqrt[]{a^2+b^2+c^2}](/latexrender/pictures/3501e3d258feb7cf848e5785ba6ae724.png) .
.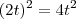

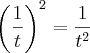
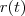 será
será ![\sqrt[]{4t^2 + 4 + \left(\frac{1}{t^2} \right)}=\sqrt[]{\frac{4t^4+4t^2+1}{t^2}} = \frac{1}{t}\sqrt[]{(2t^2 + 1)^2}=\frac{1}{t}\left(2t^2+1 \right) \sqrt[]{4t^2 + 4 + \left(\frac{1}{t^2} \right)}=\sqrt[]{\frac{4t^4+4t^2+1}{t^2}} = \frac{1}{t}\sqrt[]{(2t^2 + 1)^2}=\frac{1}{t}\left(2t^2+1 \right)](/latexrender/pictures/3b4e3c38295f76e0a14c0b034473e184.png) .
.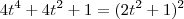 .
.
?????
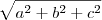 é o mesmo que a + b + c. Isso é falso! Veja um exemplo.
é o mesmo que a + b + c. Isso é falso! Veja um exemplo.
 .
.

 .
.
 :
: