 por ricardosanto » Dom Set 02, 2012 01:11
por ricardosanto » Dom Set 02, 2012 01:11
Enunciado: Calcule usando integral a região limitada pelas curvas.
2)y=9x², y=0 e x=2
eu fiz a 5º da seguinte forma:
5)y=x, y=4x²| <=> 4x²=x <=> 4x²-x=0, daí eu resolvi e encontrei os dois x, q por sua vez, são os limites desta integral ,
e faço as integrais e depois subtraio as áreas.
minha dúvida é: o que devo fazer para encontrar os limites quando a questão possui 3 igualdades?
Muito obrigado pela oportunidade de postar minhas dúvidas
Editado pela última vez por
ricardosanto em Dom Set 02, 2012 12:52, em um total de 1 vez.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por MarceloFantini » Dom Set 02, 2012 15:31
por MarceloFantini » Dom Set 02, 2012 15:31
A reta

é paralela ao eixo

. Ela encontra a parábola no ponto
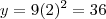
. Portanto você pode fazer

para calcular a área limitada pela curva.
No outro, os pontos de interseção tem abscissas

e
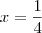
, então para calcular a área faça
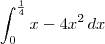
. A razão de ser
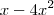
é que no intervalo
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
temos que
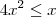
, ou seja, a bissetriz dos quadrantes ímpares está acima da parábola.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:02
- 0 Respostas
- 1127 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 23, 2014 22:02
Cálculo: Limites, Derivadas e Integrais
-
- Área limitada pelas curvas
por Fernandobertolaccini » Qua Jul 23, 2014 22:04
- 1 Respostas
- 1509 Exibições
- Última mensagem por matmatco

Sáb Ago 09, 2014 12:15
Cálculo: Limites, Derivadas e Integrais
-
- Integral, área da região limitada.
por Maicon Simoes » Qui Abr 19, 2012 10:58
- 1 Respostas
- 1931 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 15:00
Cálculo: Limites, Derivadas e Integrais
-
- Integral, achar a área da região entre as curvas
por Janoca » Sex Jun 06, 2014 17:24
- 5 Respostas
- 4948 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 21:42
Cálculo: Limites, Derivadas e Integrais
-
- Área do triângulo delimitada pelas retas r,s e t
por flaaacs » Qua Out 03, 2012 16:02
- 3 Respostas
- 3078 Exibições
- Última mensagem por young_jedi

Qua Out 03, 2012 17:25
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é paralela ao eixo
é paralela ao eixo  . Ela encontra a parábola no ponto
. Ela encontra a parábola no ponto 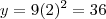 . Portanto você pode fazer
. Portanto você pode fazer  para calcular a área limitada pela curva.
para calcular a área limitada pela curva. e
e 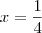 , então para calcular a área faça
, então para calcular a área faça 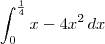 . A razão de ser
. A razão de ser 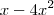 é que no intervalo
é que no intervalo ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) temos que
temos que 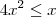 , ou seja, a bissetriz dos quadrantes ímpares está acima da parábola.
, ou seja, a bissetriz dos quadrantes ímpares está acima da parábola.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
