Bom dia . Acredito que a forma mais simples de calcular os limites sejam por L'hospital . Talvez se a indeterminação prosseguir ,terá que aplicar este teorema mais de uma vez.
OBS.: No denominador tome cuidado com a derivada . Lembre-se da regra da cadeia . Uma forma mais simples é transformar o denominador em uma composição de funções e aplicar a lei .
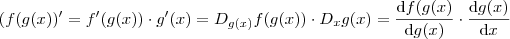
.
Se você não conseguir ,post aqui suas dúvidas .
![\lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}} \lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}}](/latexrender/pictures/e78dbfc2bdcb125b7026c207e7f66e01.png)


![\lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}} \lim_{x\to3}\frac{{x}^{2}+\sqrt[3]{x-3}-9}{\sqrt[3]{9-x\sqrt[2]{4x-3}}}](/latexrender/pictures/e78dbfc2bdcb125b7026c207e7f66e01.png)



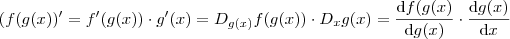 .
. 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)