 por Dankaerte » Qua Ago 26, 2009 16:49
por Dankaerte » Qua Ago 26, 2009 16:49
Se o resto da divisão do pilonômio P(x)= 2x(x está elevado a n) + 5x - 30 por Q(x)= x - 2 é igual a 44, então n é igual a ?
galera preciso da fórmula para resolver isso e se alguém poder me mostrar também por ond eu começo para resolver serei muito grato.
-
Dankaerte
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qua Ago 26, 2009 16:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qua Ago 26, 2009 18:12
por Elcioschin » Qua Ago 26, 2009 18:12
Vou dar uma dica:
+ 2*x^5 + 0*x^4 + 0*x³ + 0*x² + 5x - 30 | x - 2
_________________________________|___________________________
- 2*x^5 + 4*x^4 ........................... | 2*x^4 + 4x³ + 8*x² + 16*x + 37
___________________
......... + 4*x^4 + 0*x³
......... - 4*x^4 + 8*x³
_________________________
.................. + 8*x³ + 0*x²
.................. - 8*x³ + 16*x²
_______________________________
.......................... + 16*x² + 5*x
.......................... - 16*x² + 32*x
___________________________________
................................... + 37*x - 30
................................... - 37*x + 74
___________________________________
........................................... + 44 <------ Resto
Solução ----> n = 5
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Lucio Carvalho » Qua Ago 26, 2009 19:00
por Lucio Carvalho » Qua Ago 26, 2009 19:00
Olá Elcioschin,
Gostei muito da tua dica e apresento uma outra sugestão.
De acordo com o exercício, podemos aplicar o teorema do resto que diz: "O resto da divisão de um polinômio P(x) pelo binômio (x - a) é igual a P(a).".
Assim:

De acordo com o teorema do resto temos:
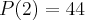
Logo:
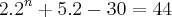



E, finalmente:

Adeus e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Elcioschin » Qua Ago 26, 2009 19:31
por Elcioschin » Qua Ago 26, 2009 19:31
Lúcio
Perfeita a sua solução.
Eu só não a coloquei, imaginando que, com a dica, o nosso colega Dankaerte chegaria nela.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Dankaerte » Qui Ago 27, 2009 14:07
por Dankaerte » Qui Ago 27, 2009 14:07
muito obrigado pela resposta de vocês, mas achei a 1ª resposta muito complicada, mas gostaria de saber Lucio se esse teorema do resto pode se aplicar em qualquer polinômio.
-
Dankaerte
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qua Ago 26, 2009 16:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qui Ago 27, 2009 18:04
por Elcioschin » Qui Ago 27, 2009 18:04
Dankaerte
1) O teorema do resto vale para qualquer polinômio (desde que seja dado o resto).
2) Quanto à primeira solução, ela não tem nada de complicado: É simplesmente o Método da Chave para divisão de polinômios, encontrado em qualquer livro ou apostila sobre o assunto.
Existem ainda outros métodos: Método de Descartes (ou dos Método dos Coeficientes a Determinar), o Teorema de D'Alembert, o Algoritmo de Briot-Ruffini e o Método de Divisão pelo Produto (x -a)*(x - b).
Sugiro a você estudar a Teoria sobre o assunto.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- preciso de ajuda urgente!!!!
 por matematicada » Qua Nov 24, 2010 12:17
por matematicada » Qua Nov 24, 2010 12:17
- 2 Respostas
- 2063 Exibições
- Última mensagem por matematicada

Qui Nov 25, 2010 11:39
Funções
-
- preciso de ajuda, é urgente
por nayane » Sex Nov 26, 2010 21:12
- 2 Respostas
- 2020 Exibições
- Última mensagem por nayane

Sáb Nov 27, 2010 14:40
Álgebra Elementar
-
- Galera preciso dessa resolução
por Justiceira » Dom Set 27, 2009 13:33
- 3 Respostas
- 2252 Exibições
- Última mensagem por Cleyson007

Dom Set 27, 2009 16:54
Trigonometria
-
- Preciso de Ajuda com Limites - URGENTE!!!
por Josi » Qui Set 10, 2009 17:34
- 4 Respostas
- 3598 Exibições
- Última mensagem por Josi

Qui Set 10, 2009 18:40
Cálculo: Limites, Derivadas e Integrais
-
- preciso de ajuda urgente por favor
por weverton » Qua Jun 23, 2010 17:56
- 0 Respostas
- 1493 Exibições
- Última mensagem por weverton

Qua Jun 23, 2010 17:56
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




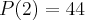
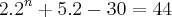






 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.