Estou com uma dúvida na seguinte questão conceitual*:
11. Suponha que
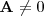 e
e  onde
onde 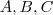 são matrizes tais que a multiplicação esteja definida.
são matrizes tais que a multiplicação esteja definida.a)
 ?
?b) Se existir uma matriz
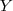 , tal que
, tal que 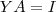 , onde
, onde 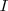 é a matriz identidade, então
é a matriz identidade, então  ?
?Bem, a resposta do item (a) é não, pois não necessariamente
 quando
quando  .
.Minha dúvida está no item (b).
Entendo que se
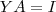 , então
, então 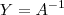 , visto que uma matriz multiplicada por sua inversa é igual à matriz identidade. No entanto, eu não sei justificar como esse fato afetaria a proposição acima, ou seja, se o fato de que a matriz
, visto que uma matriz multiplicada por sua inversa é igual à matriz identidade. No entanto, eu não sei justificar como esse fato afetaria a proposição acima, ou seja, se o fato de que a matriz 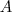 tem uma inversa teria alguma influência na proposição de que
tem uma inversa teria alguma influência na proposição de que  .
.Alguém poderia me ajudar?
*Fonte: Álgebra Linear, 3a edição, pg. 12, Ed. Harbra, Boldrini et al


 , e usando associatividade segue
, e usando associatividade segue  . Usando o fato que
. Usando o fato que 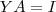 , então
, então  e
e 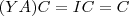 e portanto
e portanto  .
.

 é não-singular, então
é não-singular, então  implica em
implica em 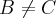 seja verdadeiro. Estou correto em afirmar isso?
seja verdadeiro. Estou correto em afirmar isso?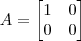 ,
, 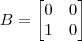 e
e 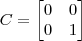 , então
, então 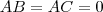 mas
mas 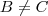 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)