 por Mariana Martin » Seg Ago 27, 2012 16:50
por Mariana Martin » Seg Ago 27, 2012 16:50
Bom dia pessoal, estou estudando inequação modular e apareceu a seguinte frase : " fazendo a intercecção com a condição de contorno". O que é condição de contorno?
Obrigada
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Ago 27, 2012 18:43
por MarceloFantini » Seg Ago 27, 2012 18:43
Mariana, por favor atente à regra número 3 do fórum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Mariana Martin » Ter Ago 28, 2012 11:52
por Mariana Martin » Ter Ago 28, 2012 11:52
Desculpe, segue abaixo o exercício:
Calcule
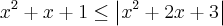
Resolução;
A função

"dentro" do módulo tem as raízes -3 e 1.
Para

, temos:

Agora eu preciso fazer a interseção com a condição de contorno e gostaria de saber como eu faço e o que é interseção com a condição de contorno, porque:
Para

Eu também preciso fazer a interseção com a condição de contorno e segundo a resolução do exercício, nesse caso a solução é vazia.
Obrigada
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Ago 28, 2012 13:43
por MarceloFantini » Ter Ago 28, 2012 13:43
Você está se perdendo em nomes. Note que a tal "condição de contorno" é a condição que você impôs para fazer suas considerações iniciais: tomou

e depois

. O que você encontrar deve, primeiro, satisfazer isto.
No primeiro caso você encontrou que
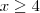
, significa que deve fazer a interseção

com

, simbolicamente
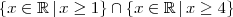
e isso dá

, pois claramente qualquer número que seja maior que quatro será maior que um, mas nem todo número maior que um será maior que quatro.
No segundo caso você também encontrou que
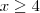
, mas a interseção

é vazia. Não existem números maiores que quatro e menores que -3.
Falta você considerar o caso em que

, de onde segue que
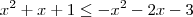
e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Mariana Martin » Ter Ago 28, 2012 14:09
por Mariana Martin » Ter Ago 28, 2012 14:09
Obrigada pela explicação, ajudou bastante.
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de Contorno
por zecamd3 » Sáb Dez 01, 2012 12:51
- 1 Respostas
- 7020 Exibições
- Última mensagem por adauto martins

Dom Out 11, 2015 15:44
Números Complexos
-
- Valor de contorno em coordenadas esféricas
por manuoliveira » Seg Jun 30, 2014 02:13
- 0 Respostas
- 1168 Exibições
- Última mensagem por manuoliveira

Seg Jun 30, 2014 02:13
Cálculo: Limites, Derivadas e Integrais
-
- Condição de Existência
por gustavowelp » Sáb Jun 26, 2010 11:56
- 5 Respostas
- 5473 Exibições
- Última mensagem por Molina

Sáb Jun 26, 2010 20:49
Logaritmos
-
- (ITA-72) Condição de Existência
por flavio2010 » Dom Jul 11, 2010 10:03
- 2 Respostas
- 4194 Exibições
- Última mensagem por Tom

Dom Jul 11, 2010 16:00
Álgebra Elementar
-
- Condição de Lipschitz
por Crist » Sex Out 24, 2014 16:24
- 2 Respostas
- 3843 Exibições
- Última mensagem por Crist

Seg Out 27, 2014 13:34
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





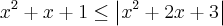
 "dentro" do módulo tem as raízes -3 e 1.
"dentro" do módulo tem as raízes -3 e 1. , temos:
, temos:


 e depois
e depois  . O que você encontrar deve, primeiro, satisfazer isto.
. O que você encontrar deve, primeiro, satisfazer isto. 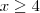 , significa que deve fazer a interseção
, significa que deve fazer a interseção  com
com  , simbolicamente
, simbolicamente 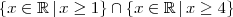 e isso dá
e isso dá  , pois claramente qualquer número que seja maior que quatro será maior que um, mas nem todo número maior que um será maior que quatro.
, pois claramente qualquer número que seja maior que quatro será maior que um, mas nem todo número maior que um será maior que quatro.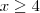 , mas a interseção
, mas a interseção  é vazia. Não existem números maiores que quatro e menores que -3.
é vazia. Não existem números maiores que quatro e menores que -3. , de onde segue que
, de onde segue que 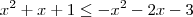 e
e  .
.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.