 por CaptainObvious » Sex Ago 17, 2012 22:05
por CaptainObvious » Sex Ago 17, 2012 22:05
Boa noite à todos no fórum. Estou trabalhando alguns exercícios de álgebra linear, e esbarrei com um problema que me gerou uma dúvida, possivelmente conceitual. A questão é a seguinte:
Mostre que para E = R^n e F = R^m temos:
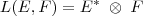
Onde L(E,F) é o espaço das aplicações lineares de E em F, E* é o dual de E e o produto entre E* e F é o produto tensorial entre os espaços.
Tentativa:
A tentativa consiste em fazer uma dupla inclusão entre os espaços, i.e., demonstrar que dado um elemento qualquer de L(E,F), este também se encontra em prodT(E*,F) e vice-versa. Se temos uma aplicação A de R^n em R^m, como afirmar que A é igual a um elemento de prodT(E*,F)? Alguém teria alguma dica?
Desde já agradeço
-
CaptainObvious
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Ago 17, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Aplicada
- Andamento: cursando
 por MarceloFantini » Sáb Ago 18, 2012 00:38
por MarceloFantini » Sáb Ago 18, 2012 00:38
O que você afirma não é verdade, estes dois espaços não são iguais. Entretanto, existe um isomorfismo entre eles, logo

. Não sei que resultados você tem ao seu dispor, mas se você notar que
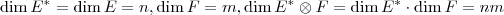
e
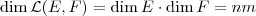
, portanto

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por CaptainObvious » Sáb Ago 18, 2012 08:45
por CaptainObvious » Sáb Ago 18, 2012 08:45
Obrigado pela resposta. Justamente isso me incomodava. Apesar de precisar provar que são iguais, não conseguia motivo algum para poder afirmá-lo. Depois de ter postado, ainda tentei uma solução um pouco menos elegante: Construir uma bijeção entre os dois espaços.
Basicamente o que fiz foi associar uma aplicação A de L(E,F), com uma aplicação f de

tal que:

onde os
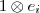
são base para

Deste modo associaremos cada aplic. de L(E,F) à uma de

tal que eles levam vetores iguais em vetores de igual representação nas respectivas bases de seus contradomínios. Acha que seguir essa linha estaria correto?
-
CaptainObvious
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Ago 17, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Aplicada
- Andamento: cursando
 por MarceloFantini » Sáb Ago 18, 2012 12:16
por MarceloFantini » Sáb Ago 18, 2012 12:16
Para mostrar que são isomorfos você precisa encontrar uma transformação linear invertível entre os dois espaços. Entretanto, acho que essa sua primeira tentativa de transformação não funciona. E lembre-se: estes dois espaços não são iguais!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicaçoes lineares (derivada)
por Zanatta » Qua Mai 15, 2013 22:59
- 0 Respostas
- 878 Exibições
- Última mensagem por Zanatta

Qua Mai 15, 2013 22:59
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicações do vetor gradiente] Aplicações das propriedades
 por TheoFerraz » Sex Out 28, 2011 16:14
por TheoFerraz » Sex Out 28, 2011 16:14
- 1 Respostas
- 3318 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:16
Cálculo: Limites, Derivadas e Integrais
-
- [Sistemas Lineares] Duvida de como resolver!!
por filipe reis farias » Sáb Mai 18, 2013 15:28
- 1 Respostas
- 2567 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 20:03
Sistemas de Equações
-
- Derivada- Como aplicar as formulas do quociente e do produto
por karinak » Sáb Jun 16, 2012 02:08
- 2 Respostas
- 1874 Exibições
- Última mensagem por karinak

Sáb Jun 16, 2012 12:43
Cálculo: Limites, Derivadas e Integrais
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4947 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
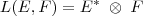


 . Não sei que resultados você tem ao seu dispor, mas se você notar que
. Não sei que resultados você tem ao seu dispor, mas se você notar que 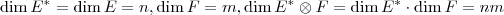 e
e 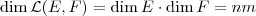 , portanto
, portanto 

 tal que:
tal que:
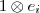 são base para
são base para 