Mostre que para E = R^n e F = R^m temos:
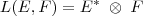
Onde L(E,F) é o espaço das aplicações lineares de E em F, E* é o dual de E e o produto entre E* e F é o produto tensorial entre os espaços.
Tentativa:
A tentativa consiste em fazer uma dupla inclusão entre os espaços, i.e., demonstrar que dado um elemento qualquer de L(E,F), este também se encontra em prodT(E*,F) e vice-versa. Se temos uma aplicação A de R^n em R^m, como afirmar que A é igual a um elemento de prodT(E*,F)? Alguém teria alguma dica?
Desde já agradeço


 . Não sei que resultados você tem ao seu dispor, mas se você notar que
. Não sei que resultados você tem ao seu dispor, mas se você notar que 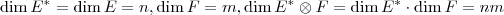 e
e 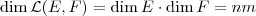 , portanto
, portanto 

 tal que:
tal que:
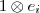 são base para
são base para 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.