 por Cleyson007 » Qui Ago 20, 2009 17:49
por Cleyson007 » Qui Ago 20, 2009 17:49
Olá, boa tarde!
Estou precisando de ajuda na resolução do exercício que segue:

Estou tentando resolver, partindo por esse raciocínio:
2B - B² = I
Colocando B em evidência --> B (2 - B) = I
Isolando o a matriz B --> B = I/(2-B)
Agradeço sua ajuda.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Lucio Carvalho » Sex Ago 21, 2009 04:40
por Lucio Carvalho » Sex Ago 21, 2009 04:40
Olá Cleyson007,
Antes de mais, usarei a notação

para a matriz inversa de B. Também deves lembrar que a matriz "I" apresentada é a matriz identidade.
Então, sabemos que:

Como tu bem sugeriste, colocamos em evidência o "B" na expressão

e ficamos com:
B.(2 - B) = I
O que está dentro de parênteses é a matriz inversa de B, ou seja,

No entanto espero a opinião dos outros participantes!
Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Cleyson007 » Sex Ago 21, 2009 14:03
por Cleyson007 » Sex Ago 21, 2009 14:03
Boa tarde Lucio!
Gostei da explicação! O que você disse faz sentido

Agora, qual seria a alternativa correta?
Não tem possui a alternativa:

Agradeço sua ajuda!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Lucio Carvalho » Sex Ago 21, 2009 15:35
por Lucio Carvalho » Sex Ago 21, 2009 15:35
Olá uma vez mais Cleyson007,
Sabendo que:

Então, penso que podemos escrever:

Assim, a opção correcta seria a alínea a)
Entretanto, espero a opinião de outros partcipantes!
Bye!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Marcampucio » Sex Ago 21, 2009 18:59
por Marcampucio » Sex Ago 21, 2009 18:59
Olá,
todo mundo chegou fácil em
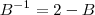
. O que falta agora é ajustar isso a uma das alternativas:
multiplicando os dois membros pela matriz identidade:

e como toda matriz quando multiplicada pela matriz identidade resulta em si mesma:

alternativa a)
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Cleyson007 » Sáb Ago 22, 2009 10:45
por Cleyson007 » Sáb Ago 22, 2009 10:45
Bom dia Lucio e Marcampucio!
Agora entendi!
Obrigado pela ajuda!!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz - Inversa ou não?
por Bruhh » Seg Mar 08, 2010 16:31
- 7 Respostas
- 16116 Exibições
- Última mensagem por Neperiano

Qui Mar 11, 2010 15:50
Conversão de Unidades
-
- [Matriz Inversa]
por vanessafey » Seg Set 12, 2011 15:17
- 4 Respostas
- 3283 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 23:23
Matrizes e Determinantes
-
- Matriz Inversa
por Claudin » Qui Set 15, 2011 17:44
- 11 Respostas
- 5274 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 18:51
Matrizes e Determinantes
-
- Inversa da Matriz
por brunojorge29 » Seg Out 10, 2011 09:48
- 4 Respostas
- 2912 Exibições
- Última mensagem por brunojorge29

Qua Out 12, 2011 17:30
Matrizes e Determinantes
-
- Matriz inversa
por ViniRFB » Sex Mar 09, 2012 14:33
- 1 Respostas
- 1397 Exibições
- Última mensagem por ViniRFB

Sex Mar 09, 2012 14:49
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 para a matriz inversa de B. Também deves lembrar que a matriz "I" apresentada é a matriz identidade.
para a matriz inversa de B. Também deves lembrar que a matriz "I" apresentada é a matriz identidade.
 e ficamos com:
e ficamos com:







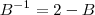 . O que falta agora é ajustar isso a uma das alternativas:
. O que falta agora é ajustar isso a uma das alternativas:





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.