 por Alane » Qui Ago 16, 2012 16:00
por Alane » Qui Ago 16, 2012 16:00
As bases de um trapézio medem 15 cm e 25 cm, e sua altura é de 16 cm. A que distância da base maior se interceptam as diagonais desse trapézio?
Fazendo uma analise, reparei que haviam dois dados nos quais eu poderia usufruir para achar a hipotenusa de um triângulo-retângulo. Então fiz: hip²= 16²+25², que deu aproximadamente 30; com isso eu dividi este resultado por 2, porque o x se encontra exatamente no meio. Contudo o resultado dessa questão é 10, não faço ideia do que fiz de errado. Alguém pode me ajudar?
- Anexos
-
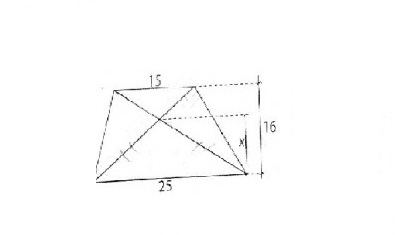
- desenho de um trapézio com seus valores e incógnita. Retirado da apostila do cursinho da Poli
- img025.jpg (9.75 KiB) Exibido 1005 vezes
-
Alane
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 05, 2012 22:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Ago 16, 2012 16:30
por e8group » Qui Ago 16, 2012 16:30
Seja o trapézio ABCD .Considere o Ponto M que interceptar as diagonais do Trapézio .
Veja que no triângulo DMC sua altura é h e no Triângulo ABM sua altura é 16 - h .
Como as bases são paralelas e as alturas são proporcionais ,assim temos que :
![\frac{25}{15}=\frac{h}{16-h} \implies 5[16-h] = 3h \implies 8h = 5(16) \implies h =10 u.c \frac{25}{15}=\frac{h}{16-h} \implies 5[16-h] = 3h \implies 8h = 5(16) \implies h =10 u.c](/latexrender/pictures/db05be561558ad92ec217fc96866b678.png)
.
Qualquer dúvida comente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Qui Ago 16, 2012 16:32
por Cleyson007 » Qui Ago 16, 2012 16:32
Boa tarde Alane!
Obrigado por retirar o enunciado em anexo. Agora posso ajudar! Vamos lá?
O Santhiago apresentou uma resolução, vou apresentar outra!
Estou no serviço e não disponibilizo de recursos para desenhar para você, mas vou tentar explicá-la escrevendo. Ok?
Seja o trapézio ABCD (esse que você anexou). Temos: Base menor AB = 15cm e base maior CD = 25cm. Trace as diagonais AD e BC , que se cruzam em O. Perceba que os triângulos AOB e COD são semelhantes (dado que o ângulo do vértice O é oposto pelo vertice e os ângulos A*D*C = B*C*D, e os outros dois pares de ângulos também são iguais (por serem alternos internos).
Logo, temos que a altura do trapézio é igual a soma das alturas desses triângulos, relativas as bases AB e DC, então sendo elas h
1 e h
2, tem-se:
h
1 + h
2 = 16 ---> h
1 = 16 - h
2 AB/CD = K (em que K é uma constante de proporcionalidade) 15/25 = k --> k = 3/5
Então,
h
1 / h
2 = 3/5
16 - h
2 / h
2 = 3/5
80 -5h
2 = 3h
2 Resolvendo, h
2 = 10cm (Relativa á base maior)
h
1 = 6cm (Relativa à base menor)
Espero que tenha ajudado.

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4668 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3506 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1925 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12649 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
-
- Teorema de Pitágoras
por Luciana Dias » Sex Mar 23, 2012 22:46
- 2 Respostas
- 1994 Exibições
- Última mensagem por Luciana Dias

Sex Mar 23, 2012 23:06
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\frac{25}{15}=\frac{h}{16-h} \implies 5[16-h] = 3h \implies 8h = 5(16) \implies h =10 u.c \frac{25}{15}=\frac{h}{16-h} \implies 5[16-h] = 3h \implies 8h = 5(16) \implies h =10 u.c](/latexrender/pictures/db05be561558ad92ec217fc96866b678.png) .
.




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.