 por Andreyan » Qui Ago 16, 2012 14:09
por Andreyan » Qui Ago 16, 2012 14:09
Olá estou com uma fórmula que foi derivada, e preciso isolar o ângulo alfa para fazer os cálculos, mas não estou conseguindo fazer essa álgebra.
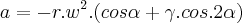
as letras r, w, e gamma são todos dados no exercicio sobrando é claro somente o alfa.
-
Andreyan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 12, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em processos de produção
- Andamento: cursando
 por MarceloFantini » Qui Ago 16, 2012 17:28
por MarceloFantini » Qui Ago 16, 2012 17:28
Andreyan, você poderia por favor postar o enunciado completo? Talvez não seja necessário isolar

, ou pior, talvez não seja possível.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Qui Ago 16, 2012 18:29
por Russman » Qui Ago 16, 2012 18:29
Note que:
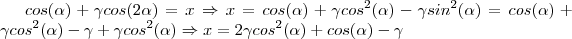
Assim, temos a seguinte equação de 2° grau:
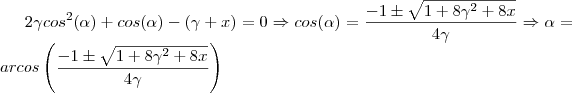
.
Como
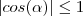
você tem de fazer um estudo para as limitações das outras constantes representadas por

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Andreyan » Sex Ago 17, 2012 12:34
por Andreyan » Sex Ago 17, 2012 12:34
Mas e em relação aos valores, de -r e W? Pq eles estão multiplicando esses cos, eles são esse x no caso que vc igualou?
-
Andreyan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Jul 12, 2011 17:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em processos de produção
- Andamento: cursando
 por Russman » Sex Ago 17, 2012 16:15
por Russman » Sex Ago 17, 2012 16:15
Isso!

.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sobre as Fórmulas
por Jhenrique » Seg Dez 10, 2012 18:29
- 3 Respostas
- 2204 Exibições
- Última mensagem por Jhenrique

Dom Fev 03, 2013 01:04
Álgebra Elementar
-
- [Editor de Fórmulas]
por dehcalegari » Ter Ago 27, 2013 11:49
- 1 Respostas
- 1403 Exibições
- Última mensagem por Cleyson007

Ter Ago 27, 2013 11:54
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração de fórmulas de derivadas
por victoreis1 » Qua Nov 24, 2010 20:09
- 1 Respostas
- 3059 Exibições
- Última mensagem por MarceloFantini

Qui Nov 25, 2010 00:43
Cálculo: Limites, Derivadas e Integrais
-
- Relação entre duas fórmulas
por FelipeScheidemantel » Qui Mar 19, 2009 19:19
- 0 Respostas
- 1758 Exibições
- Última mensagem por FelipeScheidemantel

Qui Mar 19, 2009 19:19
Álgebra Elementar
-
- Ajuda com fórmulas de crescimento econômico
por RChaves » Dom Nov 15, 2009 00:26
- 0 Respostas
- 1537 Exibições
- Última mensagem por RChaves

Dom Nov 15, 2009 00:26
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
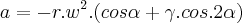

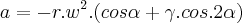

 , ou pior, talvez não seja possível.
, ou pior, talvez não seja possível.

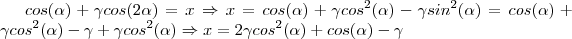
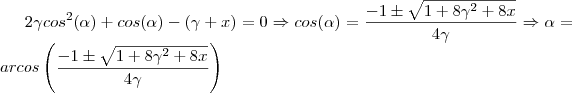 .
.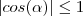 você tem de fazer um estudo para as limitações das outras constantes representadas por
você tem de fazer um estudo para as limitações das outras constantes representadas por  .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.