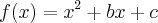 com b e c reais , tem duas raízes distintas pertencentes ao intervalo [-2,3]. Então prove que
com b e c reais , tem duas raízes distintas pertencentes ao intervalo [-2,3]. Então prove que 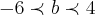 .(O sinal representa menor que.)
.(O sinal representa menor que.)Para que a função tenha duas raízes distintas
 , então
, então 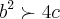 . A partir daí não sei como prosseguir. Tentei afirmar que o vértice está nesse intervalo mas não deu certo. O que devo fazer?
. A partir daí não sei como prosseguir. Tentei afirmar que o vértice está nesse intervalo mas não deu certo. O que devo fazer?

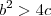 .Perceba que além disso temos que ,
.Perceba que além disso temos que , . Assim poderemos obter a seguinte inequação ,
. Assim poderemos obter a seguinte inequação ,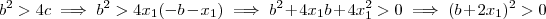

![x=\frac{-b+-\sqrt[2]{\Delta}}{2} x=\frac{-b+-\sqrt[2]{\Delta}}{2}](/latexrender/pictures/b2a9b420b43d277df8feeff04331a49c.png) Será que dá pra fazer
Será que dá pra fazer ![-2\preceq\frac{-b+-\sqrt[2]{\Delta}}{2}\preceq3 -2\preceq\frac{-b+-\sqrt[2]{\Delta}}{2}\preceq3](/latexrender/pictures/09b33cdb825d8b589d17274c6bd926cb.png) ?
?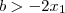 .Uma vez que
.Uma vez que ![x_1 \in [-2,3] x_1 \in [-2,3]](/latexrender/pictures/8bad8268d71146b13f148418dfb124c5.png) ,assim
,assim ![-2x_1 \in[ -6,4 ] -2x_1 \in[ -6,4 ]](/latexrender/pictures/09dea5f204455167b36932a28ab7e86c.png) .Mas como
.Mas como  ,logo concluímos que
,logo concluímos que  . Em outras palavras
. Em outras palavras  . Sendo assim provemos o que queríamos.
. Sendo assim provemos o que queríamos. ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)