 por luiz_henriquear » Ter Ago 14, 2012 00:40
por luiz_henriquear » Ter Ago 14, 2012 00:40
Meu pai propos o seguinte problema e nao consigo relacionar as variaveis:
Foi contratado um onibus para transportar ateus fervorosos em uma cidade w localizada a 150 km do destino. porem esse oninus passará em uma cidade x licalizada a 70 km dostino depois em uma cidade y a 50 km e por ultimo em uma cidade z a 30.km para q em cada uma das cidades mais ateus entrem no onibus. como a empresa de onibus foi contratada na cidade w e ela cobra por quilometragem o custo total foi de R$500,00 proporcionalmente quanto deve pagar cada cidade?
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Russman » Ter Ago 14, 2012 00:50
por Russman » Ter Ago 14, 2012 00:50
Calcula por porcentagem!
A cidade

detém
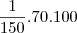
porcento do trajeto. Logo deverá pagar
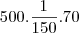
reais.
Faça o mesmo para as outras.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por luiz_henriquear » Ter Ago 14, 2012 13:20
por luiz_henriquear » Ter Ago 14, 2012 13:20
Caro, ja havia pensado dessa forma. mas e a cidade w como fica? Ela tem q pagar a maior parte, mas nao 100%
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Russman » Ter Ago 14, 2012 23:58
por Russman » Ter Ago 14, 2012 23:58
Claro que sim!
Os passageiros da cidade W pagam 500 reais divididos entre todos pois estes viajam toda kilometragem! Essa é a interpretação.
Porém, se você considerar que o total dentre todas as viagens e passageiros foi de 500 reias( oq eu acho que você fez) então
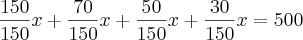
de onde
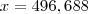
, aproximadamente.
Agora só substituir esse valor em cada parcela e calcular os valores de viagem individuais.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4487 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5524 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3338 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3582 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1547 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 detém
detém 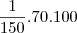 porcento do trajeto. Logo deverá pagar
porcento do trajeto. Logo deverá pagar 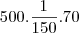 reais.
reais.
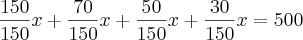
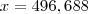 , aproximadamente.
, aproximadamente. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.