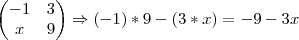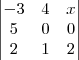por Barbara » Ter Ago 18, 2009 15:26
por Barbara » Ter Ago 18, 2009 15:26
Por favor eu preciso muito de ajuda!!!
Será que alguém poderia mu ajudar a resolver as seguintes matrizes, eh pra hj!!
2/3 1
0 3
-3 4 x
5 0 0
2 1 2
1 x 1
-2 -4 2
4 8 3
-1 3
x 9
-
Barbara
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Ago 18, 2009 15:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Ago 19, 2009 13:37
por Molina » Qua Ago 19, 2009 13:37
Barbara escreveu:Por favor eu preciso muito de ajuda!!!
Será que alguém poderia mu ajudar a resolver as seguintes matrizes, eh pra hj!!
2/3 1
0 3
-3 4 x
5 0 0
2 1 2
1 x 1
-2 -4 2
4 8 3
-1 3
x 9
Não sei se minha ajuda vai ser útil ainda, já que hoje é quarta-feira. Mas vai lá:



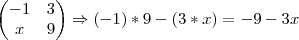
Só achei estranho que normalmente quando aparece alguma variável dentro da matriz, o exercício informa quanto vale o determinante e pede pra descobrir o valor de x.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por marciommuniz » Qua Ago 19, 2009 13:38
por marciommuniz » Qua Ago 19, 2009 13:38
Olá Bárbara, para mais informações de como resolver determinantes de ordem 2 ou 3 entre em
http://pt.wikipedia.org/wiki/Determinantelá tá bem explicadinho. Um abraço!
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Cleyson007 » Qui Ago 20, 2009 17:32
por Cleyson007 » Qui Ago 20, 2009 17:32
Boa tarde Bárbara!
O determinante de uma matriz é calculado pela diferença do produto da diagonal principal pela diagonal secundária.
Em sua 2ª dúvida:
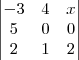
Por ser um determinante de uma matriz de ordem 3, dobra-se a primeira e a segunda coluna.

Resolvendo:

Resultado:

O link que o Marcio Muniz lhe passou é muito bom. Vale a pena conferir.

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Qui Ago 20, 2009 18:11
por Molina » Qui Ago 20, 2009 18:11
Agora que fui ver que passei a segunda questão errada por LaTeX,

Obrigado por fazê-la da forma certa, Cleyson,


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7153 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3569 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6723 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4695 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por GABRIELA » Ter Set 01, 2009 14:15
- 2 Respostas
- 2109 Exibições
- Última mensagem por GABRIELA

Ter Set 01, 2009 14:47
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.