Numa PA com números ímpar de termos, a soma dos termos de ordem ímpar é 63 e a dos termos de ordem par é 54. Achar n.
R- 13
Gostaria da ajuda de vocês para sanar minhas dúvidas já usei várias fórmulas mas nenhuma chega ao resultado correto pois é a primeira vez que resolvo esse tipo de questão...Se não for abusar da boa vontade de vocês me expliquem pois desde já fico grato
Plugpc...
.
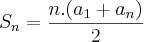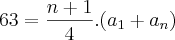e 
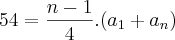
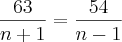
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)