 por gustavowelp » Sáb Ago 11, 2012 01:39
por gustavowelp » Sáb Ago 11, 2012 01:39
Boa noite
Estou com dificuldade em entender como há 5040 anagramas nesta questão:
Quantos anagramas que começam e terminam com a letra E podemos formar em AMBIENTE?
Não seria 2 x 6 x 5 x 4 x 3 x 2 x 1 x 1 ?
Obrigado
A resposta é 5040. Mas achei que são muitos anagramas para poucas letras....
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por e8group » Sáb Ago 11, 2012 11:16
por e8group » Sáb Ago 11, 2012 11:16
Bom dia ,para este caso só aplicar a seguinte fórmula :
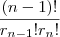
onde

e
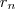
são distintos e denota repetições de determinada "letra" e

é o número de letras que compõem determinada palavra . Neste caso fica,
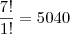
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por gustavowelp » Qua Ago 15, 2012 23:48
por gustavowelp » Qua Ago 15, 2012 23:48
Olá.
Não entendi muito bem sua resposta.
Como chegaste a 1! no denominador?
E por que n-1 no nominador?
Obrigado
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Anagrama Simples]
por gustavowelp » Sex Nov 02, 2012 12:31
- 1 Respostas
- 1636 Exibições
- Última mensagem por young_jedi

Sex Nov 02, 2012 12:46
Análise Combinatória
-
- Anagrama
por Igor » Sex Set 30, 2011 18:02
- 0 Respostas
- 1906 Exibições
- Última mensagem por Igor

Sex Set 30, 2011 18:02
Estatística
-
- [Anagrama]
por Geriane07 » Qui Ago 08, 2013 12:23
- 3 Respostas
- 1687 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 02, 2013 09:06
Análise Combinatória
-
- Dúvida anagrama
por renataf » Ter Dez 07, 2010 08:47
- 2 Respostas
- 2266 Exibições
- Última mensagem por renataf

Dom Jan 02, 2011 13:45
Estatística
-
- Permutação-Anagrama
por Alessandra Cezario » Ter Jan 31, 2012 13:32
- 1 Respostas
- 1720 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:20
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


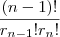 onde
onde  e
e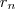 são distintos e denota repetições de determinada "letra" e
são distintos e denota repetições de determinada "letra" e  é o número de letras que compõem determinada palavra . Neste caso fica,
é o número de letras que compõem determinada palavra . Neste caso fica,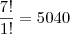


 .
.



