 por Rafael16 » Qua Ago 08, 2012 13:19
por Rafael16 » Qua Ago 08, 2012 13:19
Boa tarde

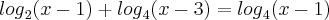
--> Mudei a base do primeiro logaritmo para 4
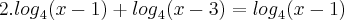
![{log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1) {log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1)](/latexrender/pictures/0bb3baedd2dbc1a2dbcdc2577054d68c.png)
--> Cancelando os log, cheguei no polinômio
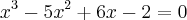
Não estudei polinômios ainda. Gostaria de saber se até onde cheguei esta certo, e também, se tem uma outra forma de resolver isso?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por e8group » Qua Ago 08, 2012 15:17
por e8group » Qua Ago 08, 2012 15:17
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Ago 08, 2012 15:43
por e8group » Qua Ago 08, 2012 15:43
A maneira a qual você resolveu estar correta também , entretanto há um risco de você comete um erro assumindo x= 1 .
Veja :
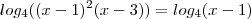
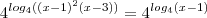
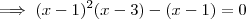
![(x-1)\left[(x-1)(x-3) -1 \right] (x-1)\left[(x-1)(x-3) -1 \right]](/latexrender/pictures/9cad2e3a2a466fadd5dee6edf7471ff6.png)
Agora perceba que ,
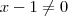
.Logo ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2469 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1874 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1461 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1676 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1824 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

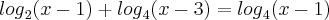 --> Mudei a base do primeiro logaritmo para 4
--> Mudei a base do primeiro logaritmo para 4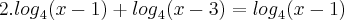
![{log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1) {log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1)](/latexrender/pictures/0bb3baedd2dbc1a2dbcdc2577054d68c.png) --> Cancelando os log, cheguei no polinômio
--> Cancelando os log, cheguei no polinômio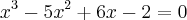


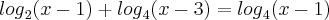 --> Mudei a base do primeiro logaritmo para 4
--> Mudei a base do primeiro logaritmo para 4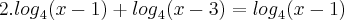
![{log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1) {log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1)](/latexrender/pictures/0bb3baedd2dbc1a2dbcdc2577054d68c.png) --> Cancelando os log, cheguei no polinômio
--> Cancelando os log, cheguei no polinômio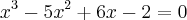

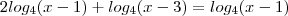
![log_4\left[\frac{(x-1)^2 \cdot(x-3)}{(x-1)}\right] =0 ; x\neq 1 log_4\left[\frac{(x-1)^2 \cdot(x-3)}{(x-1)}\right] =0 ; x\neq 1](/latexrender/pictures/3ed48b3078fa6ff00003429a92cb1660.png)
![\implies log_4\left[(x-1)\cdot(x-3)\right] =0 \implies log_4\left[(x-1)\cdot(x-3)\right] =0](/latexrender/pictures/e605391ffbe3efaee2c7a8e22db5cd88.png)
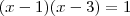

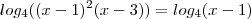
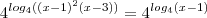
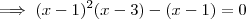
![(x-1)\left[(x-1)(x-3) -1 \right] (x-1)\left[(x-1)(x-3) -1 \right]](/latexrender/pictures/9cad2e3a2a466fadd5dee6edf7471ff6.png)
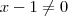 .Logo ,
.Logo , .
.