
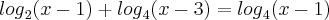 --> Mudei a base do primeiro logaritmo para 4
--> Mudei a base do primeiro logaritmo para 4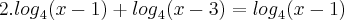
![{log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1) {log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1)](/latexrender/pictures/0bb3baedd2dbc1a2dbcdc2577054d68c.png) --> Cancelando os log, cheguei no polinômio
--> Cancelando os log, cheguei no polinômio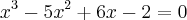
Não estudei polinômios ainda. Gostaria de saber se até onde cheguei esta certo, e também, se tem uma outra forma de resolver isso?


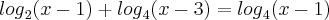 --> Mudei a base do primeiro logaritmo para 4
--> Mudei a base do primeiro logaritmo para 4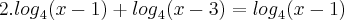
![{log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1) {log}_{4}[(x-1)^2(x-3)]={log}_{4}(x-1)](/latexrender/pictures/0bb3baedd2dbc1a2dbcdc2577054d68c.png) --> Cancelando os log, cheguei no polinômio
--> Cancelando os log, cheguei no polinômio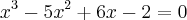

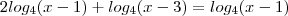
![log_4\left[\frac{(x-1)^2 \cdot(x-3)}{(x-1)}\right] =0 ; x\neq 1 log_4\left[\frac{(x-1)^2 \cdot(x-3)}{(x-1)}\right] =0 ; x\neq 1](/latexrender/pictures/3ed48b3078fa6ff00003429a92cb1660.png)
![\implies log_4\left[(x-1)\cdot(x-3)\right] =0 \implies log_4\left[(x-1)\cdot(x-3)\right] =0](/latexrender/pictures/e605391ffbe3efaee2c7a8e22db5cd88.png)
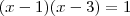

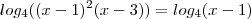
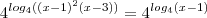
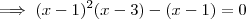
![(x-1)\left[(x-1)(x-3) -1 \right] (x-1)\left[(x-1)(x-3) -1 \right]](/latexrender/pictures/9cad2e3a2a466fadd5dee6edf7471ff6.png)
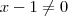 .Logo ,
.Logo , .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)