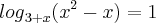
 ---> Aqui tenho uma dúvida, não sei se posso passar x² para o 1° membro, ou se posso deixar no 2° mesmo, pois a concavidade muda
---> Aqui tenho uma dúvida, não sei se posso passar x² para o 1° membro, ou se posso deixar no 2° mesmo, pois a concavidade muda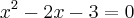 --> X'= -1 e x''=3
--> X'= -1 e x''=3Os valores de x satisfazem as condições de existência da base e do logaritmando. Portanto S = {-1,3}
Mas a resposta do meu esta S = {3}



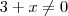 e
e 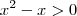 . A solução
. A solução  serve, mas
serve, mas 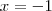 não.
não.

 e
e 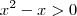 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)