 por emsbp » Seg Jul 16, 2012 17:56
por emsbp » Seg Jul 16, 2012 17:56
Boa tarde. Como posso resolver o seguinte exercício:
«A reta de equação y=-2x+1 é assíntota do gráfico de uma função f, de domínio

. Qual o valor de

»
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por skin » Seg Jul 16, 2012 21:06
por skin » Seg Jul 16, 2012 21:06
emsbp escreveu:Boa tarde. Como posso resolver o seguinte exercício:
«A reta de equação y=-2x+1 é assíntota do gráfico de uma função f, de domínio

. Qual o valor de

»
Obrigado!
Veja,
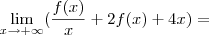

e como

é assintota de

significa que

.
Para resolver
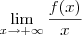
vc pode usar L'Hopital.
Espero que ajude.
Editado pela última vez por
skin em Seg Jul 16, 2012 21:11, em um total de 1 vez.
-
skin
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Jul 15, 2012 21:19
- Localização: Campinas
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Russman » Seg Jul 16, 2012 21:08
por Russman » Seg Jul 16, 2012 21:08
Você sabe o que é uma assíntota?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por skin » Seg Jul 16, 2012 21:11
por skin » Seg Jul 16, 2012 21:11
Russman escreveu:Você sabe o que é uma assíntota?

-
skin
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Jul 15, 2012 21:19
- Localização: Campinas
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por e8group » Seg Jul 16, 2012 21:19
por e8group » Seg Jul 16, 2012 21:19
seria ?

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jul 16, 2012 21:31
por Russman » Seg Jul 16, 2012 21:31
skin escreveu:Russman escreveu:Você sabe o que é uma assíntota?

Eu perguntei para o criador do tópico! kk
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por skin » Ter Jul 17, 2012 01:50
por skin » Ter Jul 17, 2012 01:50
santhiago escreveu:seria ?

Santhiago,

apenas no infinito, por isso escrevemos

.
Só um detalhe....
-
skin
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Jul 15, 2012 21:19
- Localização: Campinas
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por emsbp » Ter Jul 17, 2012 08:55
por emsbp » Ter Jul 17, 2012 08:55
Sim, sei o que é uma assintota.
No problema que vos dei, trata-se de uma assintota não vertical, mais concretamente uma assintota oblíqua.
Como temos Y=-2x+1, o declive (m), desta reta será -2, donde m=
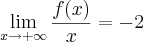
.
Substituindo, no limite pedido fico com -2+
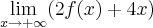
.
A partir daqui, a minha dúvida reside no cálculo do limite que ficou.
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por e8group » Ter Jul 17, 2012 10:53
por e8group » Ter Jul 17, 2012 10:53
emsbp , acho que você pode fazer assim (vamos ver que os demais usuário acham ) ,
![- 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ] - 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ]](/latexrender/pictures/10950c46e97688ae63d2b9fdf7d06879.png)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por skin » Ter Jul 17, 2012 15:44
por skin » Ter Jul 17, 2012 15:44
emsbp escreveu:-2+
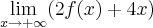
.
A partir daqui, a minha dúvida reside no cálculo do limite que ficou.
Obrigado!
Para calcular esse limite, vc precisa usar a informação da assíntota, i.e,

.
Veja:

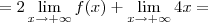

![=\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2 =\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2](/latexrender/pictures/f30d3c424a620b76ae9c31ba65c47317.png)

-
skin
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Jul 15, 2012 21:19
- Localização: Campinas
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - Assintotas
por Viviani » Qui Jan 10, 2013 13:19
- 2 Respostas
- 1839 Exibições
- Última mensagem por Viviani

Ter Jan 15, 2013 16:12
Cálculo: Limites, Derivadas e Integrais
-
- [limite] assintotas duvida
 por beel » Ter Set 06, 2011 13:37
por beel » Ter Set 06, 2011 13:37
- 2 Respostas
- 1537 Exibições
- Última mensagem por beel

Dom Out 16, 2011 16:57
Cálculo: Limites, Derivadas e Integrais
-
- assíntotas
 por pseytow » Qua Jul 02, 2008 13:11
por pseytow » Qua Jul 02, 2008 13:11
- 2 Respostas
- 5478 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:39
Cálculo: Limites, Derivadas e Integrais
-
- assíntotas
por aquis » Qua Set 10, 2014 11:49
- 0 Respostas
- 1643 Exibições
- Última mensagem por aquis

Qua Set 10, 2014 11:49
Cálculo: Limites, Derivadas e Integrais
-
- Limites(assíntotas)
por Luciano Dias » Dom Jan 03, 2010 12:37
- 3 Respostas
- 7582 Exibições
- Última mensagem por Molina

Dom Jan 03, 2010 23:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Qual o valor de
. Qual o valor de  »
»
 . Qual o valor de
. Qual o valor de  »
»
. Qual o valor de
»
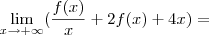

 é assintota de
é assintota de significa que
significa que  .
.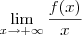 vc pode usar L'Hopital.
vc pode usar L'Hopital.






 apenas no infinito, por isso escrevemos
apenas no infinito, por isso escrevemos  .
.
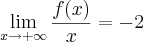 .
.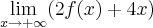 .
.
![- 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ] - 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ]](/latexrender/pictures/10950c46e97688ae63d2b9fdf7d06879.png)

.
 .
.
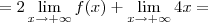

![=\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2 =\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2](/latexrender/pictures/f30d3c424a620b76ae9c31ba65c47317.png)



 .
.



