«A reta de equação y=-2x+1 é assíntota do gráfico de uma função f, de domínio
 . Qual o valor de
. Qual o valor de  »
»Obrigado!

 . Qual o valor de
. Qual o valor de  »
»
emsbp escreveu:Boa tarde. Como posso resolver o seguinte exercício:
«A reta de equação y=-2x+1 é assíntota do gráfico de uma função f, de domínio. Qual o valor de
»
Obrigado!
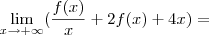

 é assintota de
é assintota de significa que
significa que  .
.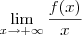 vc pode usar L'Hopital.
vc pode usar L'Hopital.

Russman escreveu:Você sabe o que é uma assíntota?




skin escreveu:Russman escreveu:Você sabe o que é uma assíntota?

santhiago escreveu:seria ?
 apenas no infinito, por isso escrevemos
apenas no infinito, por isso escrevemos  .
.
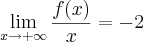 .
.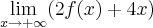 .
.
![- 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ] - 2 + \lim_{x\to +\infty} \left(2f(x) + 4x\right) = -2 + \lim_{x\to +\infty} \left[x \left(2\frac{f(x)}{x} + 4\right)\right ]](/latexrender/pictures/10950c46e97688ae63d2b9fdf7d06879.png)

emsbp escreveu:-2+.
A partir daqui, a minha dúvida reside no cálculo do limite que ficou.
Obrigado!
 .
.
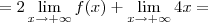

![=\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2 =\lim_{x\rightarrow+\infty}[2(-2x+1)+4x]=2](/latexrender/pictures/f30d3c424a620b76ae9c31ba65c47317.png)


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes