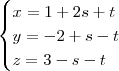
Não sei como transformar para forma cartesiana, seria uma passagem de paramétricas para equação cartesiana?

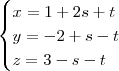

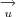 perpendicular ao plano;
perpendicular ao plano;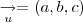 ;
;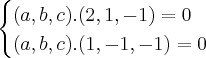
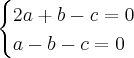
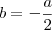 e
e 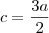
 ,
, 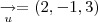
 , então,
, então, 
 é obtido substituindo o ponto do plano
é obtido substituindo o ponto do plano 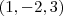 na equação, portanto,...
na equação, portanto,...
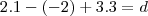

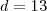


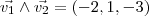 ,
,
 pertence ao plano, temos
pertence ao plano, temos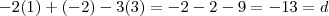 ,
, , ou multiplicando por menos um para trocar o sinal,
, ou multiplicando por menos um para trocar o sinal,  .
.

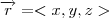 é o raio-vetor do espaço
é o raio-vetor do espaço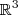 , então, se
, então, se 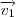 ,
, 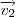 e
e 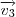 são vetores constantes, a equação vetorial do plano é dada por
são vetores constantes, a equação vetorial do plano é dada por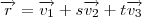 ,
, e
e  são parâmetros.
são parâmetros.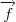 , de forma que
, de forma que 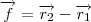 ,
,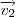 e
e 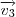 são a base de qualquer outro vetor pertencente a esse plano! Veja,
são a base de qualquer outro vetor pertencente a esse plano! Veja,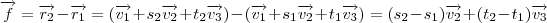 .
.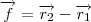 é combinação linear dos vetores acima. Logo estes são base para o espaço entendido pelo plano e , portanto, seus chamados vetores diretores!
é combinação linear dos vetores acima. Logo estes são base para o espaço entendido pelo plano e , portanto, seus chamados vetores diretores! que seja normal ao plano é obtido tomando
que seja normal ao plano é obtido tomando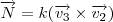 ,
,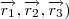 e obtendo o vetor normal
e obtendo o vetor normal  da seguinte forma
da seguinte forma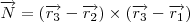 .
.



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



