 por TuTa » Qui Jul 12, 2012 00:22
por TuTa » Qui Jul 12, 2012 00:22
To emperrando nuns exercicios envolvendo limites com funcoes trigonometricas
1)O valor de

Tentei separar os limites
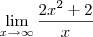
e
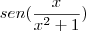
, mas continuava dando indeterminações.
Tem outro na mesma linha:
2)
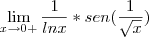
Eu me enrosco todo quando tem esses limites com funçoes trigonometricas. Qual seria o macete para resolve-los?
-
TuTa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 24, 2012 16:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Qui Jul 12, 2012 00:58
por e8group » Qui Jul 12, 2012 00:58
1)
Faça

, daí :
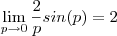
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por TuTa » Qui Jul 12, 2012 01:33
por TuTa » Qui Jul 12, 2012 01:33
Poha que sacada! Vlw santhiago
Ah vc usou a identidade:

E nesse aki? ln 0??
2)
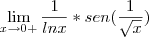
-
TuTa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 24, 2012 16:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Qui Jul 12, 2012 12:13
por e8group » Qui Jul 12, 2012 12:13
TuTa escreveu:E nesse aki? ln 0??
Não !
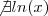
para

entretanto

,perceba que
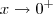
está em uma " vizinhança " do zero ,neste caso estar bem próximo a direita do zero .
Faça uma análise ,
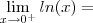
"

" , note que "

" não é um número ,é apenas uma notação para denotar o comportamento que ln(x) " estar bem distante do zero a esquerda " .
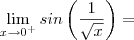
"

" , perceba que "

" não tem como definir . Entretanto sabemos que
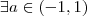
tal que
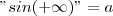
.
Agora ,
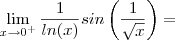
"

" "

" = "
" "

" . Independente de
![a \in (-1,0] a \in (-1,0]](/latexrender/pictures/5edac53094a8d8618592bd8c5870ec6f.png)
ou
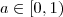
, temos que :

.
Conclusão não existe o limite , pois os limites laterais diferem e além disso só está definido na parte real apenas valores positivos não nulos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3423 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4187 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3135 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3384 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2991 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

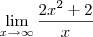 e
e 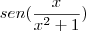 , mas continuava dando indeterminações.
, mas continuava dando indeterminações.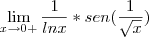


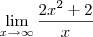 e
e 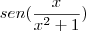 , mas continuava dando indeterminações.
, mas continuava dando indeterminações.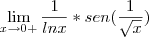

 , daí :
, daí : 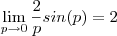


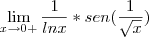

 para
para  entretanto
entretanto  ,perceba que
,perceba que  está em uma " vizinhança " do zero ,neste caso estar bem próximo a direita do zero .
está em uma " vizinhança " do zero ,neste caso estar bem próximo a direita do zero .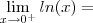 "
"  " , note que "
" , note que " " não é um número ,é apenas uma notação para denotar o comportamento que ln(x) " estar bem distante do zero a esquerda " .
" não é um número ,é apenas uma notação para denotar o comportamento que ln(x) " estar bem distante do zero a esquerda " . 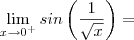 "
"  " , perceba que "
" , perceba que " " não tem como definir . Entretanto sabemos que
" não tem como definir . Entretanto sabemos que 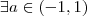 tal que
tal que 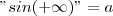 .
. 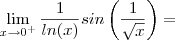 "
" " "
" " " = "
" = " 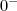 " "
" " " . Independente de
" . Independente de ![a \in (-1,0] a \in (-1,0]](/latexrender/pictures/5edac53094a8d8618592bd8c5870ec6f.png) ou
ou 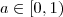 , temos que :
, temos que : .
.

 .
.
 :
: