 por Rafael16 » Qui Jul 05, 2012 12:01
por Rafael16 » Qui Jul 05, 2012 12:01
Na inequação
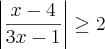
Para (I):
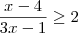
Para (II):
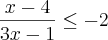
Depois faz a UNIÃO das soluções de cada inequação que fica
S = {
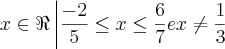
}
Na inequação
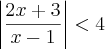
A solução é
S= {
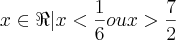
}
O que eu não entendi foi que na primeira inequação, para achar a solução, usa-se a UNIÃO, e na segunda inequação usa-se a INTERSECÇÃO.Por que não pode usar união?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Qui Jul 05, 2012 13:20
por Russman » Qui Jul 05, 2012 13:20
Para a primeira equação, ou
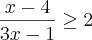
ou
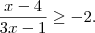
Da primeira,
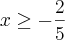
. E da segunda,
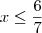
.
Assim, se você desenhar os intervalos vera que se unem de forma que
![{x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]} {x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]}](/latexrender/pictures/45484fb6cdc689ccbcdaeb82ec959770.png)
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Jul 05, 2012 13:33
por Russman » Qui Jul 05, 2012 13:33
Na segunda as soluções são
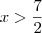
e
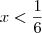
.
Unindo os intervalos, temos
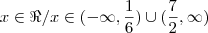
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7387 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- inequação modular
por manuoliveira » Dom Ago 22, 2010 22:30
- 1 Respostas
- 3472 Exibições
- Última mensagem por Dan

Seg Ago 23, 2010 15:38
Álgebra Elementar
-
- Inequação modular
por scggomes » Qui Abr 21, 2011 17:22
- 3 Respostas
- 3204 Exibições
- Última mensagem por MarceloFantini

Qui Abr 21, 2011 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Inequação Modular
por Rafael16 » Qui Mar 08, 2012 20:24
- 2 Respostas
- 2414 Exibições
- Última mensagem por Rafael16

Qui Mar 08, 2012 21:21
Funções
-
- inequação modular
por haiashi » Qua Jun 06, 2012 00:33
- 0 Respostas
- 1545 Exibições
- Última mensagem por haiashi

Qua Jun 06, 2012 00:33
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

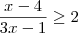
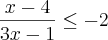
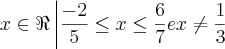 }
}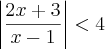
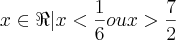 }
}

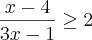
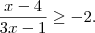
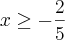 . E da segunda,
. E da segunda, 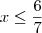 .
.![{x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]} {x \in \Re / x \in [ -\frac{2}{5} , \frac{1}{3}) \cup (\frac{1}{3} ,\frac{6}{7}]}](/latexrender/pictures/45484fb6cdc689ccbcdaeb82ec959770.png) .
.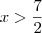 e
e 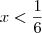 .
.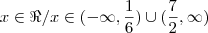
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.