 por TAE » Ter Jul 03, 2012 20:14
por TAE » Ter Jul 03, 2012 20:14
Olá, boa noite,
Na figura ao lado temos
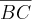
paralelo de
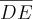
a) Calcule o valor de x.

Uploaded with
ImageShack.usEu tinha tentado:
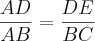
Mas não deu certo.
Valeu.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por MarceloFantini » Ter Jul 03, 2012 22:19
por MarceloFantini » Ter Jul 03, 2012 22:19
Por favor, mostre todas suas contas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por TAE » Qua Jul 04, 2012 00:28
por TAE » Qua Jul 04, 2012 00:28
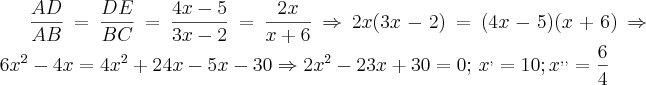
A resposta é 10 (no livro = x`), mas não poderia ser 6/4= x``?
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por e8group » Qua Jul 04, 2012 10:39
por e8group » Qua Jul 04, 2012 10:39
TAE escreveu:A resposta é 10 (no livro = x`), mas não poderia ser 6/4= x``?
Observe o segmento AD e reflita por que "não poderia ser 6/4= x`` " ,logo descobrirá o motivo lógico .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por TAE » Qui Jul 05, 2012 20:28
por TAE » Qui Jul 05, 2012 20:28
Então é por percepção, valeu.
AD=10; BD=-6; AD=1, realmente não faz sentido.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Semelhança
 por anniewallker » Sex Jan 13, 2012 14:19
por anniewallker » Sex Jan 13, 2012 14:19
- 4 Respostas
- 3898 Exibições
- Última mensagem por anniewallker

Sex Jan 13, 2012 19:37
Trigonometria
-
- Semelhança
por TAE » Qui Jun 21, 2012 23:10
- 5 Respostas
- 5366 Exibições
- Última mensagem por TAE

Ter Jun 26, 2012 22:02
Geometria Plana
-
- Semelhança de triangulos
 por DanielRJ » Ter Dez 28, 2010 19:30
por DanielRJ » Ter Dez 28, 2010 19:30
- 7 Respostas
- 5485 Exibições
- Última mensagem por Otavio Rubiao

Qui Jan 27, 2011 10:36
Geometria Plana
-
- Semelhança de triângulos
 por igorcamilo » Sáb Jun 04, 2011 19:55
por igorcamilo » Sáb Jun 04, 2011 19:55
- 1 Respostas
- 2443 Exibições
- Última mensagem por Adriano Tavares

Dom Jan 01, 2012 14:55
Geometria Plana
-
- Semelhança de triângulos
por Gaussiano » Sáb Dez 10, 2011 13:59
- 0 Respostas
- 1588 Exibições
- Última mensagem por Gaussiano

Sáb Dez 10, 2011 13:59
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
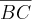 paralelo de
paralelo de 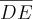

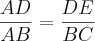

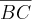 paralelo de
paralelo de 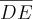

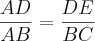


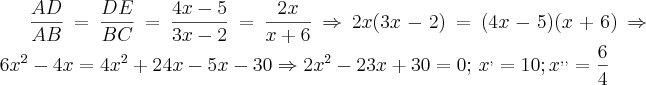




 .
.
 :
: