Russman escreveu:A teoria garante que a função é extrema no ponto em que f'(x) = 0.
Cuidado! A teoria não garante isso.
Por exemplo, para a função

temos que
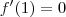
. Entretanto, no ponto x = 1 não temos nem máximo e nem mínimo para essa função.
O correto seria dizer algo como: "
a teoria garante que a função pode ser extrema no ponto em que f'(x) = 0".
Observe que "
pode ser" e "
é" são coisas bem distintas!
allakyhero escreveu:Estou estudando "Valores Máximo e Mínimo" com auxilio de um livro, até esse momento compreendo a questão de que cavidade para cima é máximo e cavidade para baixo é mínimo etc...
Só que não compreendo como faço a resolução do problema.
Por exemplo, a questão 49 do livro.
49. f(x) = 3x² - 12x + 5, [0, 3]
f'(x) = 6x¹ - 12, [0, 3]
f'(x) = 6x - 12 = 0
Depois dai não sei o que fazer...
Alguém poderia me auxiliar?
Observe que o exercício lhe forneceu uma função (no caso, f(x) = 3x² - 12x + 5) e um intervalo (no caso, [0, 3]).
Nesse contexto, a ideia é usar o chamado "Método do Intervalo Fechado" para resolver o exercício. Para saber mais a respeito desse método, eu gostaria de recomendar que você assista a videoaula "19. Cálculo I - Máximo e Mínimo de Funções". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoQuanto a última passagem que você postou, perceba que:

Como você exibiu dúvidas na resolução dessa equação, eu aproveito para recomendar que você assista também a videoaula "Matemática Zero - Aula 13 - Equação do Primeiro Grau". Ela esta disponível no canal do Nerckie no YouTube:
http://www.youtube.com/nerckieEu espero que as videoaulas indicas possam lhe ajudar a tirar suas dúvidas.





 temos que
temos que 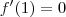 . Entretanto, no ponto x = 1 não temos nem máximo e nem mínimo para essa função.
. Entretanto, no ponto x = 1 não temos nem máximo e nem mínimo para essa função.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.