 por Vitor2+ » Sáb Jun 30, 2012 23:04
por Vitor2+ » Sáb Jun 30, 2012 23:04
Estou com dúvida a respeito da questão indicada abaixo. Resolvi a mesma, porém, como o professosr não deu o gabarito da questão não sei se a resoluçaõ está certa. Alguém poderia indicar se existe algo errado ou se a questão está correta? Agradeço
CALCULE AS DERIVADAS PARCIAIS DE 2ª ORDEM DA FUNÇÃO f(x,y)=cos(x³+xy):
Resolução:
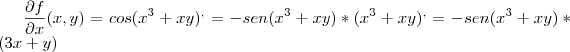
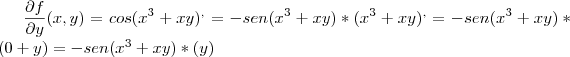

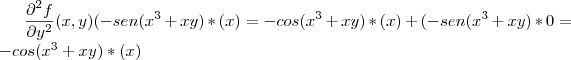
[/tex]
-
Vitor2+
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Nov 14, 2011 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por brunoiria » Dom Jul 01, 2012 00:57
por brunoiria » Dom Jul 01, 2012 00:57
sim, tem erros em
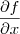
ao derivar

isso da

;

ao derivar

isso da

;
consequentemente vc errou

e

, reveja ai;
e esta faltando as parciais mistas, boa sorte ai
-
brunoiria
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Jun 23, 2012 10:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic Mat
- Andamento: cursando
 por LuizAquino » Dom Jul 01, 2012 10:29
por LuizAquino » Dom Jul 01, 2012 10:29
Vitor2+ escreveu:Estou com dúvida a respeito da questão indicada abaixo. Resolvi a mesma, porém, como o professosr não deu o gabarito da questão não sei se a resoluçaõ está certa. Alguém poderia indicar se existe algo errado ou se a questão está correta? Agradeço
CALCULE AS DERIVADAS PARCIAIS DE 2ª ORDEM DA FUNÇÃO f(x,y)=cos(x³+xy):
Resolução:
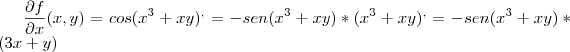
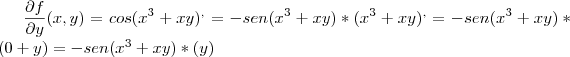

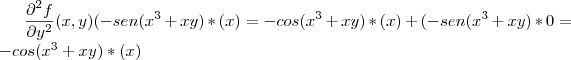
[/tex]
Eu gostaria de lhe dar uma dica para estudar a resolução de uma derivada. Você pode usar um programa para isso! Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a resolução de

.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
d^2/dx^2 cos(x^3 + xy)
- Clique no botão de igual ao lado do campo de entrada.
- Após a derivada ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada Parcial de 1ª Ordem] - Derivada parcial num ponto
por Vitor2+ » Dom Jul 01, 2012 16:27
- 6 Respostas
- 4789 Exibições
- Última mensagem por e8group

Seg Jul 02, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- derivada parcial de segunda ordem
por gregorylino » Qui Set 26, 2013 11:39
- 1 Respostas
- 1785 Exibições
- Última mensagem por gregorylino

Qui Set 26, 2013 16:39
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Parcial] Pedido de ajuda para resolução
por itsdeas » Sex Nov 07, 2014 18:21
- 3 Respostas
- 3164 Exibições
- Última mensagem por young_jedi

Seg Nov 10, 2014 20:25
Cálculo: Limites, Derivadas e Integrais
-
- [derivada parcial] duvida no enunciado da questao
por ricardosanto » Sáb Jun 02, 2012 00:32
- 4 Respostas
- 2686 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 02, 2012 18:56
Cálculo: Limites, Derivadas e Integrais
-
- Questão regra da cadeia - Derivada parcial
por Sobreira » Qua Mar 13, 2013 00:59
- 1 Respostas
- 3374 Exibições
- Última mensagem por young_jedi

Qui Mar 14, 2013 11:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
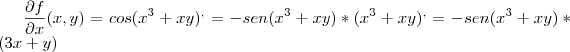
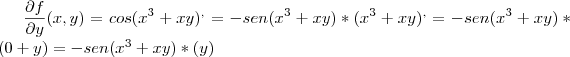

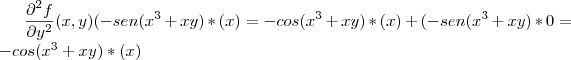

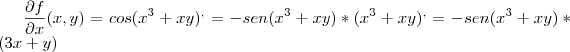
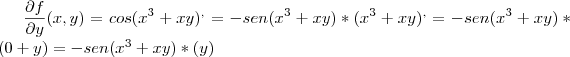

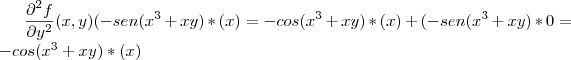

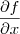 ao derivar
ao derivar  isso da
isso da  ;
; ao derivar
ao derivar  isso da
isso da  ;
; e
e  , reveja ai;
, reveja ai;
 .
.
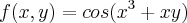 :
: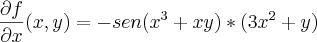



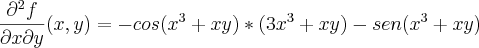
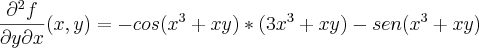

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.