 , onde
, onde 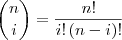 e a notação
e a notação 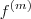 significa derivar a função
significa derivar a função  m-vezes .
m-vezes .Alguém sabe como provar por indução ?
Grato desde já !

 , onde
, onde 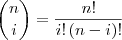 e a notação
e a notação 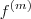 significa derivar a função
significa derivar a função  m-vezes .
m-vezes .
 ?
?


 . Este é o primeiro passo para usar indução finita.
. Este é o primeiro passo para usar indução finita.

 sim ! , veja :
sim ! , veja : 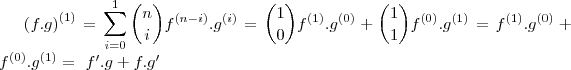



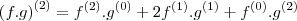 .
. . é verdadeiro .
. é verdadeiro . vamos provar para
vamos provar para  .
.
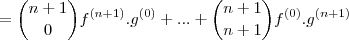


 não é necessário provar para
não é necessário provar para  . Até aí você estava certo, mas quando fez a igualdade
. Até aí você estava certo, mas quando fez a igualdade 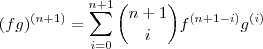 errou, pois isto é o que você quer provar. Você deve sair de um dos lados da igualdade e chegar no outro, não assumir que é válido.
errou, pois isto é o que você quer provar. Você deve sair de um dos lados da igualdade e chegar no outro, não assumir que é válido.


![(fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}] (fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}]](/latexrender/pictures/ec0e2f518705fdefea260ca4776ad26c.png)



 .
.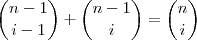 (Triângulo de Pascal )
(Triângulo de Pascal )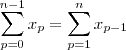
 .
. .
. 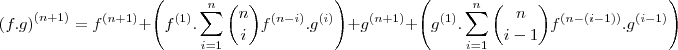
 .
.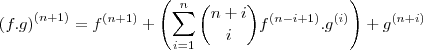 .
.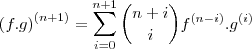 .
.
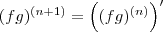 . Sua primeira solução está correta.
. Sua primeira solução está correta.

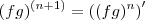 (que é verdadeiro) e que
(que é verdadeiro) e que 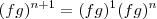 (falso ) ,neste caso eu acredito que a solução do "brunoiria" estar correta .Vou fazer novamente o mesmo .
(falso ) ,neste caso eu acredito que a solução do "brunoiria" estar correta .Vou fazer novamente o mesmo .
![\left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/e3acca6a485bec6fa55359e310a710de.png) .
.![\left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/47d6a34c5e87329e2129e352cd41a8e9.png) , que foi exatamente que o " brunoiria " fez acima . abraços a todos !
, que foi exatamente que o " brunoiria " fez acima . abraços a todos !
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)