 por e8group » Qua Jun 27, 2012 21:28
por e8group » Qua Jun 27, 2012 21:28
Prove (por indução ) a fórmula de Leibniz

, onde
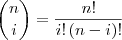
e a notação
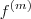
significa derivar a função

m-vezes .
Alguém sabe como provar por indução ?
Grato desde já !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Jun 27, 2012 23:21
por MarceloFantini » Qua Jun 27, 2012 23:21
Santhiago, o que você tentou? Provou o caso

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qua Jun 27, 2012 23:29
por e8group » Qua Jun 27, 2012 23:29
Sim ,meu objetivo é provar para n = 1,2,3,4,...,n . Infelizmente não estou conseguindo agora , mas vou continuar tentando até amanha eu posto minha dificuldades .obrigado pela atenção !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Jun 27, 2012 23:31
por MarceloFantini » Qua Jun 27, 2012 23:31
Eu perguntei se você conseguiu fazer a demonstração para

. Este é o primeiro passo para usar indução finita.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qui Jun 28, 2012 10:15
por e8group » Qui Jun 28, 2012 10:15
ah ! para

sim ! , veja :
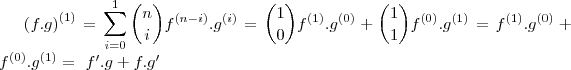
indução finita seria fazer n = (1,2,3,4,5, ..., n) ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Jun 28, 2012 21:41
por e8group » Qui Jun 28, 2012 21:41
Continuando ....
para


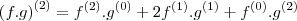
.
Para

. é verdadeiro .
Supondo a validade para

vamos provar para

.

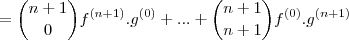
Estou no caminho certo ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Jun 28, 2012 21:43
por e8group » Qui Jun 28, 2012 21:43
Exercício sem resposta no livro ,não sei como que fica .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Jun 29, 2012 01:31
por MarceloFantini » Sex Jun 29, 2012 01:31
Depois de provar para

não é necessário provar para

. Até aí você estava certo, mas quando fez a igualdade
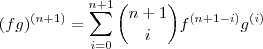
errou, pois isto é o que você quer provar. Você deve sair de um dos lados da igualdade e chegar no outro, não assumir que é válido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Sex Jun 29, 2012 10:24
por e8group » Sex Jun 29, 2012 10:24
Marcelo Fantini , obrigado pela atenção . Qualquer evolução no exercício eu posto aqui .abraços .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por brunoiria » Sex Jun 29, 2012 19:02
por brunoiria » Sex Jun 29, 2012 19:02
bom ,eu pensei em fazer assim
![(fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}] (fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}]](/latexrender/pictures/ec0e2f518705fdefea260ca4776ad26c.png)
derivando cada termo e reagrupando

-
brunoiria
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Jun 23, 2012 10:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic Mat
- Andamento: cursando
 por e8group » Sáb Jun 30, 2012 09:58
por e8group » Sáb Jun 30, 2012 09:58
brunoiria ,tudo bem ? obrigado pela solução ! Também tive esta ideia mas acho que "escapa " um pouco da expressão geral .abraços .Em breve posto minha solução .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Jun 30, 2012 10:49
por e8group » Sáb Jun 30, 2012 10:49
Bom ,acho que agora foi !!!
Continuando ....
para

.
Propriedades
I)
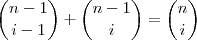
(Triângulo de Pascal )
ii)
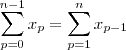
Solução :

.
Aplicando a distributividade de produto ,temos :

.
Usando propriedade ii) ,temos :
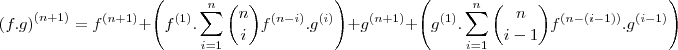

.
Usando a Relação (Stifel) ,obtemos :
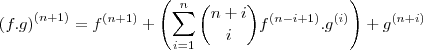
.
Reagrupando o Somatório :
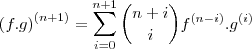
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Jun 30, 2012 12:00
por MarceloFantini » Sáb Jun 30, 2012 12:00
Cuidado! Você não está multiplicando derivadas. A notação confundiu você, perceba que
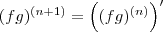
. Sua primeira solução está correta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Sáb Jun 30, 2012 12:19
por e8group » Sáb Jun 30, 2012 12:19
Marcelo Fantini ,mais uma vez obrigado .realmente a notação me confundiu ,entrei em contradição orá achei que
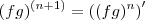
(que é verdadeiro) e que
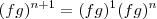
(falso ) ,neste caso eu acredito que a solução do "brunoiria" estar correta .Vou fazer novamente o mesmo .
OBS.: Exercício trabalhoso, (talvez pelo fato de ser o primeiro exercício de indução finita que faço!) mas divertido .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Jul 01, 2012 15:53
por e8group » Dom Jul 01, 2012 15:53
Consegui concluir para n+1 .
![\left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/e3acca6a485bec6fa55359e310a710de.png)
.
Expandirmos o somatório e derivando cada termo e reagrupando ,concluímos
![\left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/47d6a34c5e87329e2129e352cd41a8e9.png)
, que foi exatamente que o " brunoiria " fez acima . abraços a todos !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Indução] Prove para todo n inteiro
por +danile10 » Qua Fev 13, 2013 19:46
- 1 Respostas
- 1720 Exibições
- Última mensagem por +danile10

Qua Fev 13, 2013 20:05
Conjuntos
-
- Notação de leibniz {dúvida}
por Danilo » Sáb Abr 27, 2013 13:15
- 2 Respostas
- 2559 Exibições
- Última mensagem por Danilo

Sáb Abr 27, 2013 15:54
Cálculo: Limites, Derivadas e Integrais
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Prove: n(A X B) = n(A) * n(B)
por juliomarcos » Dom Set 14, 2008 02:58
- 3 Respostas
- 5271 Exibições
- Última mensagem por admin

Qua Set 24, 2008 05:33
Conjuntos
-
- Prove que
por Balanar » Dom Ago 29, 2010 17:22
- 1 Respostas
- 2309 Exibições
- Última mensagem por MarceloFantini

Seg Ago 30, 2010 01:24
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , onde
, onde 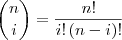 e a notação
e a notação 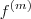 significa derivar a função
significa derivar a função  m-vezes .
m-vezes .
 , onde
, onde 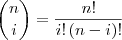 e a notação
e a notação 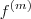 significa derivar a função
significa derivar a função  m-vezes .
m-vezes .
 ?
?


 . Este é o primeiro passo para usar indução finita.
. Este é o primeiro passo para usar indução finita.

 sim ! , veja :
sim ! , veja : 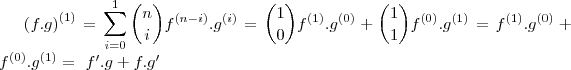



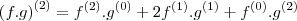 .
. . é verdadeiro .
. é verdadeiro . vamos provar para
vamos provar para  .
.
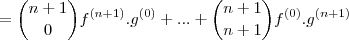


 não é necessário provar para
não é necessário provar para  . Até aí você estava certo, mas quando fez a igualdade
. Até aí você estava certo, mas quando fez a igualdade 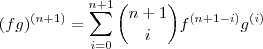 errou, pois isto é o que você quer provar. Você deve sair de um dos lados da igualdade e chegar no outro, não assumir que é válido.
errou, pois isto é o que você quer provar. Você deve sair de um dos lados da igualdade e chegar no outro, não assumir que é válido.


![(fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}] (fg)^{(n+1)}=D[(fg)^{n}]=D[\sum_{i}^{n} \binom{n}{i}f^{(n-i)}g^{(i)}] = D[f^{(n)}g]+D[nf^{(n-1)}g^{(1)}]+\dots+D[nf^{(1)}g^{(n-1)}]+D[fg^{(n)}]](/latexrender/pictures/ec0e2f518705fdefea260ca4776ad26c.png)



 .
.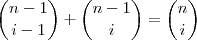 (Triângulo de Pascal )
(Triângulo de Pascal )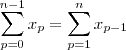
 .
. .
. 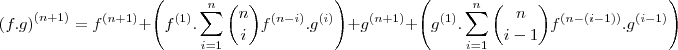
 .
.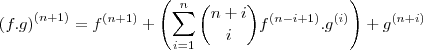 .
.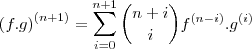 .
.
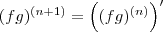 . Sua primeira solução está correta.
. Sua primeira solução está correta.

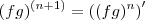 (que é verdadeiro) e que
(que é verdadeiro) e que 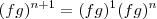 (falso ) ,neste caso eu acredito que a solução do "brunoiria" estar correta .Vou fazer novamente o mesmo .
(falso ) ,neste caso eu acredito que a solução do "brunoiria" estar correta .Vou fazer novamente o mesmo .
![\left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = D\left[\sum_{i=0}^{n} \binom{n}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/e3acca6a485bec6fa55359e310a710de.png) .
.![\left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right] \left(fg\right)^{n+1} = \sum_{i=0}^{n+1} \binom{n+1}{i} f^{n-i} g^{i} \right]](/latexrender/pictures/47d6a34c5e87329e2129e352cd41a8e9.png) , que foi exatamente que o " brunoiria " fez acima . abraços a todos !
, que foi exatamente que o " brunoiria " fez acima . abraços a todos !
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
