 por Anderson Alves » Ter Abr 17, 2012 22:30
por Anderson Alves » Ter Abr 17, 2012 22:30
Olá Pessoal.
Tenho dúvidas neste exercício.
1) Em uma progressão aritmética de razão 3, a soma do 5º com o 10º termo é 19. A soma de seus 16 primeiros termos vale quanto?
Resp.: 200
O problema é chegar neste resultado. Fiz das maneiras possíveis de, com fórmulas, e não consegui chegar a este resultado.
Ficarei grato pela ajuda....
-
Anderson Alves
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Sex Fev 24, 2012 22:39
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
 por fraol » Ter Abr 17, 2012 22:56
por fraol » Ter Abr 17, 2012 22:56
Anderson Alves escreveu: Em uma progressão aritmética de razão 3, a soma do 5º com o 10º termo é 19. A soma de seus 16 primeiros termos vale quanto?

( r = razão = 3 )

como
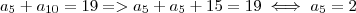
então


.
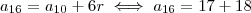
.
Agora você pode calcular a soma:
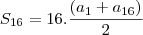
, ok?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por vanezainferniza » Qui Jun 21, 2012 17:24
por vanezainferniza » Qui Jun 21, 2012 17:24
O computador de marcela foi comprado em 1° de março de 2008?
Continuação - e sofreu depreciação de R$ 25,00 a cada mês. Sabendo que 1° de março de 2010 esse computador foi avaliado em R$ 800,00, escreva o termo geral de uma PA que expresse seu valor a cada mês. Depois determine o valor desse computador em 1° de julho de 2008 ?
-
vanezainferniza
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 21, 2012 17:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qui Jun 21, 2012 21:46
por Russman » Qui Jun 21, 2012 21:46
Eu tenho uma solução diferente.
O problema informa que

.
Lembrando que,
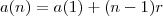
então

.
Agora,
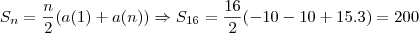
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões aritméticas
por Alessandrasouza » Sex Mai 14, 2010 15:44
- 3 Respostas
- 2068 Exibições
- Última mensagem por Cleyson007

Sáb Mai 15, 2010 10:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 07, 2012 01:13
- 2 Respostas
- 1309 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 07, 2012 01:31
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Dom Abr 08, 2012 21:10
- 2 Respostas
- 1630 Exibições
- Última mensagem por Anderson Alves

Qui Abr 12, 2012 22:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 14, 2012 13:42
- 1 Respostas
- 1666 Exibições
- Última mensagem por Lucio Carvalho

Sáb Abr 14, 2012 16:46
Progressões
-
- Progressões Aritméticas
por MarinaM » Dom Abr 15, 2012 00:24
- 2 Respostas
- 1825 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 19:56
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ( r = razão = 3 )
( r = razão = 3 ) como
como 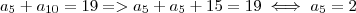

 .
.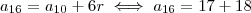 .
.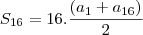 , ok?
, ok?

 .
.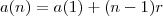
 .
.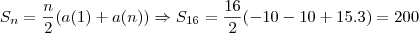 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

