 por citadp » Qua Jun 20, 2012 11:42
por citadp » Qua Jun 20, 2012 11:42
quando diz estude os extremos de uma função sem darem um intervalo ou ponto, basta calcular os zeros da derivada e ver onde são esses zeros?
Ou como se faz ?
Na função

dizem-me para calcular em IR, só calculo com os zeros da derivada ?
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Qua Jun 20, 2012 13:17
por e8group » Qua Jun 20, 2012 13:17
Seja g uma função ,onde
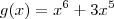
.Para estudarmos o extremos desta função, basta descobrir os pontos críticos de
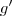
e analisa-os .

.
pontos críticos :

.
Teste da derivada segunda :
em

não podemos afirmar nada ,entretanto quando
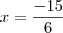
g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,
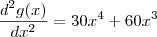
e portanto
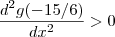
o que significa que há um ponto de mínimo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] extremos;ponto de minimo e maximo
por beel » Dom Out 30, 2011 19:15
- 2 Respostas
- 2141 Exibições
- Última mensagem por LuizAquino

Seg Out 31, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2007 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] Ponto minimo/máximo e concavidade
por gabriel feron » Dom Out 07, 2012 03:52
- 1 Respostas
- 2200 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- Questão de Máximo e Mínimo Global - Calculo I
por Mai96 » Qua Jul 08, 2015 22:12
- 2 Respostas
- 1739 Exibições
- Última mensagem por adauto martins

Qui Jul 16, 2015 18:39
Cálculo: Limites, Derivadas e Integrais
-
- Máximo e mínimo
por thadeu » Qua Nov 18, 2009 13:47
- 1 Respostas
- 4163 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 17:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 dizem-me para calcular em IR, só calculo com os zeros da derivada ?
dizem-me para calcular em IR, só calculo com os zeros da derivada ?
 dizem-me para calcular em IR, só calculo com os zeros da derivada ?
dizem-me para calcular em IR, só calculo com os zeros da derivada ?
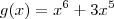 .Para estudarmos o extremos desta função, basta descobrir os pontos críticos de
.Para estudarmos o extremos desta função, basta descobrir os pontos críticos de 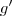 e analisa-os .
e analisa-os . .
. .
. não podemos afirmar nada ,entretanto quando
não podemos afirmar nada ,entretanto quando 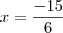 g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,
g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,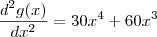 e portanto
e portanto 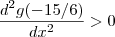 o que significa que há um ponto de mínimo .
o que significa que há um ponto de mínimo .