 por emsbp » Qui Jun 07, 2012 17:57
por emsbp » Qui Jun 07, 2012 17:57
Boa tarde. Necessito de ajuda no seguinte problema:
«O Nuno, para se deslocar de casa para a escola, costuma ir no carro da mãe ou de camioneta. O horário de trabalho da mãe permite-lhe ir com ela 76% das vezes. Como o trânsito está cada vez mais complicado, a probabilidade de chegar atrasado às aulas, independentemente do transporte utilizado é de 15%. A probabilidade de chegar atrasado e ir com a mãe é de 7%. Determine a probabilidade de o Nuno ir de camioneta e chegar atrasado.»
Comecei por tentar representar a informação num diagrama de Venn, mas estou com dificuldades em representar toda a informação.
Obrigado.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por joaofonseca » Qui Jun 07, 2012 21:34
por joaofonseca » Qui Jun 07, 2012 21:34
emsbp escreveu:A probabilidade de chegar atrasado e ir com a mãe é de 7%. Determine a probabilidade de o Nuno ir de camioneta e chegar atrasado.
A redação desta parte está correcta?
Eu perguntaria qual probabilidaade de chegar atrasado, dado ter ido de camioneta?
Os acontecimentos "ir de camioneta" e "chegar atrasado as aulas"
não são acontecimentos independentes. Porque existe uma razão de causualidade entre os dois.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por emsbp » Sex Jun 08, 2012 07:34
por emsbp » Sex Jun 08, 2012 07:34
Sim, está correta. Transcrevi tal e qual como está no manual.
Obrigado.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por joaofonseca » Sex Jun 08, 2012 10:49
por joaofonseca » Sex Jun 08, 2012 10:49
Assim sendo, sejam dois acontecimentos:
A-"O Nuno vai de carro para a escola"
"O Nuno vai de camioneta para a escola" será o acontecimento contrário.
B-"O Nuno chega atrasado às aulas"
Sabemos que

e

.
Deste tipo de exercicios também sabemos que

. Está conclusão pode ser obtida através da construção de uma tabela ou de um diagrama em árvore. Agora basta substituir com os valores conhecidos e resolver em ordem a
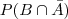
.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por emsbp » Ter Jun 12, 2012 07:14
por emsbp » Ter Jun 12, 2012 07:14
Bom dia.
Muito obrigado. Faltava-me chegar a [quote="joaofonseca"]Assim sendo, sejam dois acontecimentos:
Deste tipo de exercicios também sabemos que

.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por SARAABRANCO » Qua Jun 13, 2012 17:57
por SARAABRANCO » Qua Jun 13, 2012 17:57
estou com duvidas nestes exercicios gostava que me ajudassem pf:
- no bar de uma escola estão à venda 5 tipos de pasteis (laranja, feijão, nata, coco e amendoa). 4 amigos, joao, maria , paulo e rui , decidem comer um pastel cada um. o joao escolhe pastel de laranja ou de feijao. a maria nao escolhe pastel de nata. de quantas maneiras diferentes podem ser escolhidos os pasteis?
eu pensei assim: o joao tem 2 hipoteses de pastel , a maria tem 3 (pois no total eram 4 pois ela nao come o pastel de nata mas como o joao ja tinnha escolhido um, seriam 3) e os outros dois 2! e depois multiplicando tudo por 4x4 pois a ordem de escolha de cada um poderia ser de 4 maneiras diferentes para cada um deles) . nao sei o qe pensei de errado..
- numa confenrencia de alto nivel encontram-se 12 politicos de 4 paises sendo 3 de cada país. de quantas maneiras diferentes podem disporse as 12 pessoas em fila para uma foto de modo que os representantes de cada pais fiquem juntos?
para esta eu raciocinei assim: primeiro sabemos que temos que aglomerar 12 pessoas em 4 grupos (4 paises) e sabemos que dentro de cada grupo as posieçoes mudam 3! . depois multiplicaria tudo por 4 pois sao 4 grupos...
- 3 raparigas e os respectivos namorados posam p uma foto. de quantas maneiras se podem dispor, lado a lado, de modo que cada par de namorados fique junto na foto?
aqui eu pensei que temos que aglomerar 6 pessoas em grupos de 2, send que dentr de cada grupo podese mudar de posiçoes 2 vezes
agradeço sugestoes ! obrigadaa
-
SARAABRANCO
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 13, 2012 17:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema em Probabilidades
por Brainwreck » Qua Ago 31, 2011 19:45
- 1 Respostas
- 1667 Exibições
- Última mensagem por Caradoc

Qua Ago 31, 2011 22:47
Estatística
-
- [Probabilidades e análise combinatória] Problema
por fff » Qua Mar 05, 2014 16:59
- 0 Respostas
- 1302 Exibições
- Última mensagem por fff

Qua Mar 05, 2014 16:59
Análise Combinatória
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2950 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
-
- probabilidades
 por edwilsoncrep » Qui Mar 04, 2010 19:28
por edwilsoncrep » Qui Mar 04, 2010 19:28
- 3 Respostas
- 3274 Exibições
- Última mensagem por edwilsoncrep

Qui Mar 04, 2010 19:49
Estatística
-
- Probabilidades!
por pferraz » Qui Out 27, 2011 22:53
- 3 Respostas
- 7062 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:04
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  .
. . Está conclusão pode ser obtida através da construção de uma tabela ou de um diagrama em árvore. Agora basta substituir com os valores conhecidos e resolver em ordem a
. Está conclusão pode ser obtida através da construção de uma tabela ou de um diagrama em árvore. Agora basta substituir com os valores conhecidos e resolver em ordem a 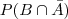 .
.

 .
.



