




 , x é dado por:
, x é dado por:

 , substituir x por t e encontrar y.
, substituir x por t e encontrar y.



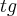 envolvida, ai não sei como chegar na resposta correta.
envolvida, ai não sei como chegar na resposta correta.




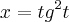
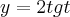


Claudin escreveu:Alguém conseguiu chegar no resultado como o gabarito? Ainda não consegui compreender.
 .
.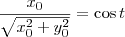
 . Temos então que:
. Temos então que: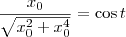


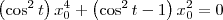
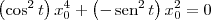
![\left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0 \left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0](/latexrender/pictures/36f378826e63d9169ae06d62187e1677.png)
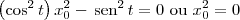
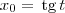 ou
ou 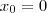 .
. , temos que
, temos que 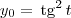 ou
ou  .
.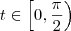 podemos obter as seguintes equações paramétricas para o "lado direito" da parábola:
podemos obter as seguintes equações paramétricas para o "lado direito" da parábola: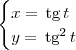
![t\in \left(\frac{\pi}{2}, \pi\right] t\in \left(\frac{\pi}{2}, \pi\right]](/latexrender/pictures/a87757804020e851a25a8dd3e87fbaec.png) as equações paramétricas para o "lado esquerdo" da parábola também serão essas.
as equações paramétricas para o "lado esquerdo" da parábola também serão essas. pode ter equações paramétricas dadas por:
pode ter equações paramétricas dadas por: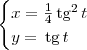
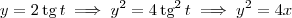
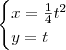
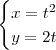


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.