Existem duas formas, na minha opinião, de resolver esse problema. A primeira é observando o comportamento do volume de óleo do tanque para um número finito de golpes. Este, a fim de identificar um padrão e modelar uma função
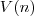
que calcule o volume de óleo do tanque após o n-ésimo golpe. A segunda forma é identificar uma relação básica de recorrência, que existe pro trás do problema, e solucioná-la.
Pela primeira forma:
Veja que
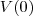
representa o volume inicial de óleo no tanque, isto é, antes de iniciados os golpes. Portanto, temos a sequência de

volumes sucessivos de óleo no tanque dada por
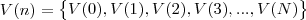
Como cada golpe extrai 10% do volume do tanque, então temos, para
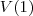
a relação
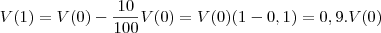
.
Para
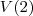
então teremos
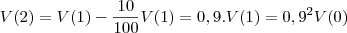
.
Você não tardará em perceber que é válida para esta a relação
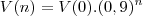
.
Pela segunda forma:
É fato que o volume de óleo no tanque do n-ésimo golpe tira 10% do volume de óleo que existia no tanque após o (n-1)-ésimo golpe. Assim, temos a seguinte equação recorrênte:
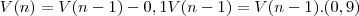
.
Para solução desta suponhamos uma função do tipo
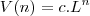
, onde c é uma constante arbitrária e L um valor a ser determinado real ou complexo. Aplicando esta hipótese na equação obtemos
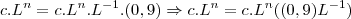
.
Supondo que
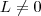
, pois nesse caso a solução seria trivial, podemos simplificar
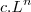
na equação e obtemos
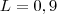
.
Portanto a solução da equação é
![[tex]V(n) = c.(0,9)^{n} [tex]V(n) = c.(0,9)^{n}](/latexrender/pictures/c4d92f69fe12e2278fb2e1865f14c3d4.png)
[/tex] onde
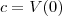
, pois
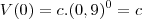
.
Exatamente a mesma solução que obtivemos por inspeção!
Para resolver a letra a) basta susbtituir

.
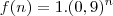


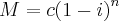

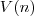 que calcule o volume de óleo do tanque após o n-ésimo golpe. A segunda forma é identificar uma relação básica de recorrência, que existe pro trás do problema, e solucioná-la.
que calcule o volume de óleo do tanque após o n-ésimo golpe. A segunda forma é identificar uma relação básica de recorrência, que existe pro trás do problema, e solucioná-la.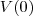 representa o volume inicial de óleo no tanque, isto é, antes de iniciados os golpes. Portanto, temos a sequência de
representa o volume inicial de óleo no tanque, isto é, antes de iniciados os golpes. Portanto, temos a sequência de  volumes sucessivos de óleo no tanque dada por
volumes sucessivos de óleo no tanque dada por 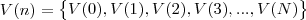
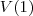 a relação
a relação 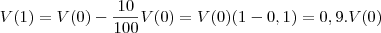 .
.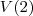 então teremos
então teremos 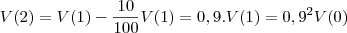 .
.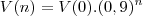 .
.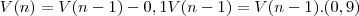 .
.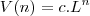 , onde c é uma constante arbitrária e L um valor a ser determinado real ou complexo. Aplicando esta hipótese na equação obtemos
, onde c é uma constante arbitrária e L um valor a ser determinado real ou complexo. Aplicando esta hipótese na equação obtemos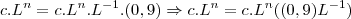 .
.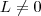 , pois nesse caso a solução seria trivial, podemos simplificar
, pois nesse caso a solução seria trivial, podemos simplificar 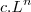 na equação e obtemos
na equação e obtemos 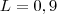 .
.![[tex]V(n) = c.(0,9)^{n} [tex]V(n) = c.(0,9)^{n}](/latexrender/pictures/c4d92f69fe12e2278fb2e1865f14c3d4.png) [/tex] onde
[/tex] onde 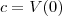 , pois
, pois 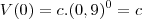 .
. .
.
 .
.
 :
: