 por Cleyson007 » Ter Jun 12, 2012 15:47
por Cleyson007 » Ter Jun 12, 2012 15:47
Boa tarde a todos!
Mostre que
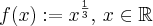
, não é diferenciável em

.
Bom, sei que se os limites laterais forem diferentes a função não é diferenciável. Mas os limites laterais em questão são iguais. Como prosseguir?
Obs.: Encontrei os limites pela direita e pela esquerda:
![\lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})} \lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/ed008f8b430a66900bc2543860199715.png)
e pela esquerda
![\lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})} \lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/c25ae20232c4d5fb8cc1f9b98deb8644.png)
Como prosseguir nesse caso em que os limites laterais são iguais?
Ficarei grato se alguém puder me ajudar.
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por e8group » Ter Jun 12, 2012 17:37
por e8group » Ter Jun 12, 2012 17:37
Boa tarde Cleyson007 .
como ,

Analizando f' , notamos que em x = 0 f'(x) converge para "mais infinito " .ou seja f' é descontinua em x = 0. Portanto a função f defenida por f(x) não é diferenciável em x = 0.
abraços !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por joaofonseca » Ter Jun 12, 2012 19:22
por joaofonseca » Ter Jun 12, 2012 19:22
A forma mais facil de concluir que a função f não é diferenciável no ponto de abcissa x=0, é:
1)Observar o gráfico:
Como se observa e pode concluir, o declive da reta tangente ao gráfico em x=0 é infinito, logo (para muitos autores) não existe derivada.
2)Obter a expressão da 1ª derivada de f, através das regras de diferenciação e chegar à mesma conclusão que o santhiago chegou.
Optando por utilizar a definição de derivada, fica:
![f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h} f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}](/latexrender/pictures/b835fdbf067d311aa0f94cb6f7a77296.png)
Agora aplica-se a diferença de cubos para eliminar as raízes cúbicas, multiplicando numerador e denominador por:
![\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2} \sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}](/latexrender/pictures/5647619fe9cd7bdcba4255fbe0ffb38e.png)
Depois de simplificar, ficamos com:
![f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right) f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right)](/latexrender/pictures/30d4d786d56c9e5470f58c780a046988.png)
A partir daqui é facil.Mas isto não é a definição de derivada num ponto!!!
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Diferenciabilidade] função diferenciável
por -civil- » Qui Set 29, 2011 14:50
- 1 Respostas
- 1552 Exibições
- Última mensagem por LuizAquino

Sex Set 30, 2011 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Função diferenciável
por fff » Sáb Set 27, 2014 18:31
- 0 Respostas
- 1130 Exibições
- Última mensagem por fff

Sáb Set 27, 2014 18:31
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração continuidade de uma função diferenciável
por Beatriz4 » Sáb Abr 28, 2012 20:58
- 1 Respostas
- 1650 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 01:40
Cálculo: Limites, Derivadas e Integrais
-
- DERIVADAS PARCIAIS e continuidade - função é diferenciável?
por inkz » Seg Nov 26, 2012 20:37
- 3 Respostas
- 5993 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 00:01
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade, Derivada Parcial e Função Diferenciável]
por raimundoocjr » Qui Out 24, 2013 17:28
- 0 Respostas
- 1169 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 17:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
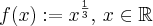 , não é diferenciável em
, não é diferenciável em  .
.![\lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})} \lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/ed008f8b430a66900bc2543860199715.png) e pela esquerda
e pela esquerda ![\lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})} \lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/c25ae20232c4d5fb8cc1f9b98deb8644.png)




![f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h} f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}](/latexrender/pictures/b835fdbf067d311aa0f94cb6f7a77296.png)
![\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2} \sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}](/latexrender/pictures/5647619fe9cd7bdcba4255fbe0ffb38e.png)
![f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right) f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right)](/latexrender/pictures/30d4d786d56c9e5470f58c780a046988.png)





