 por e8group » Qua Jun 06, 2012 11:37
por e8group » Qua Jun 06, 2012 11:37
um farol ,situado a 1000 m de uma costa (praticamente) reta está girando com uma velocidade de 3rpm (rotações por minuto)
.Qual a velocidade da luz do farol na região costeira quando o ângulo entre o feixe de luz e a perpendicular do farol à praia é de

(resposta 300 pi m/min) ?
Tentativa de solução :
primeiramente ,considerei um ponto (P) no espaço de modo que sua distância a costa seja ortogonal e equivale 1000 m.
A parti de P a luz se propaga de modo retilineo em sentido a região costeira cujo o Ângulo de incidência é igual a pi/4 .
com essas ideias ,utilizei Pitágoras no Triângulo retângulo e derivei cada parcela em relação ao tempo e achei uma resposta que difere do gabarito .
Alguém poderia sugerir alguma ideia p/ resolver este exercício ?
Obrigado.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por hygorvv » Qua Jun 06, 2012 17:05
por hygorvv » Qua Jun 06, 2012 17:05
santhiago escreveu:um farol ,situado a 1000 m de uma costa (praticamente) reta está girando com uma velocidade de 3rpm (rotações por minuto)
.Qual a velocidade da luz do farol na região costeira quando o ângulo entre o feixe de luz e a perpendicular do farol à praia é de

(resposta 300 pi m/min) ?
Tentativa de solução :
primeiramente ,considerei um ponto (P) no espaço de modo que sua distância a costa seja ortogonal e equivale 1000 m.
A parti de P a luz se propaga de modo retilineo em sentido a região costeira cujo o Ângulo de incidência é igual a pi/4 .
com essas ideias ,utilizei Pitágoras no Triângulo retângulo e derivei cada parcela em relação ao tempo e achei uma resposta que difere do gabarito .
Alguém poderia sugerir alguma ideia p/ resolver este exercício ?
Obrigado.
Sendo x a hipotenusa, e k a distancia percorrida na costa, temos:
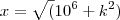
mas,

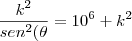


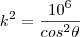
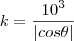
mas,
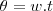
e

, logo,

assim
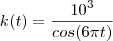
Derivando em relação ao tempo, temos:

mas
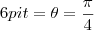
Logo
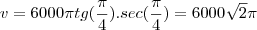
m/min
Não sei onde errei (se errei), espero que te ajude em algo.
-
hygorvv
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Jun 05, 2012 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Qua Jun 06, 2012 21:39
por e8group » Qua Jun 06, 2012 21:39
Hygorvv,Muito Obrigado pela atenção .Eu tinha resolvido desta forma e achei a mesma resposta que você ,entretanto fiz o exercício novamente e achei uma resposta diferente da sua e inclusive do gabarito .
![\theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min \theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min](/latexrender/pictures/6bec866b50b5eaa2552bba52c475dcc5.png)
Sera que estar certo ?
Alguém pode ajudar,por favor?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qui Jun 07, 2012 00:15
por Russman » Qui Jun 07, 2012 00:15
Você precisa calcular o módulo do vetor velocidade, que é indicado pelo vetor azul na imagem. Este é,
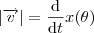
.
Da imagem notamos que o valor

é dado por

.
Assim,

.
Portanto, visto que
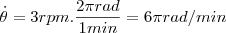
, temos para

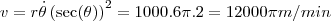
.
- Anexos
-

- ScreenHunter_02 Jun. 06 22.58.gif (2.67 KiB) Exibido 2537 vezes
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Qui Jun 07, 2012 12:44
por e8group » Qui Jun 07, 2012 12:44
Russman,Muito obrigado .Então, minha solução está correta e neste caso o gabarito errado .
Como você fez para gera a imagem ? qual aplicativo usou ?
Abraços !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60613 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5494 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10632 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8463 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
-
- taxa de variacao
por cal12 » Dom Nov 27, 2011 16:46
- 3 Respostas
- 5404 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 22:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (resposta 300 pi m/min) ?
(resposta 300 pi m/min) ?

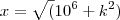

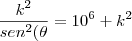


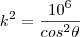
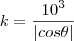
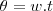 e
e  , logo,
, logo, 
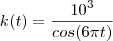

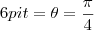
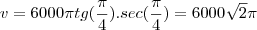 m/min
m/min
![\theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min \theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min](/latexrender/pictures/6bec866b50b5eaa2552bba52c475dcc5.png)
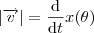 .
. é dado por
é dado por .
. .
.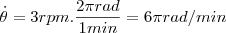 , temos para
, temos para 
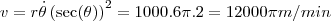 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

