 por TAE » Qua Jun 06, 2012 19:16
por TAE » Qua Jun 06, 2012 19:16
Olá, Boa noite, como resolve:
![1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0 1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0](/latexrender/pictures/ad45e81e28805e8c29af8efdbf2dcfcd.png)
Certo até aqui?
Resposta:
x=6
Valeu.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por Russman » Qua Jun 06, 2012 23:08
por Russman » Qua Jun 06, 2012 23:08
Não!
Veja que
![{(-\sqrt[]{{x}^{2}-11})}^{2} = \left|{x}^{2}-11 \right| {(-\sqrt[]{{x}^{2}-11})}^{2} = \left|{x}^{2}-11 \right|](/latexrender/pictures/43fa8852cb028aa21e21d3eed107c182.png)
.
Assim,
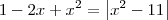
.
Se

, isto é,
![x>\sqrt[]{11}\simeq3,3166 x>\sqrt[]{11}\simeq3,3166](/latexrender/pictures/fdd1826941c4141b5776552083be6382.png)
então temos a equação
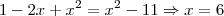
Veja qe o valor calculado cumpre a condição inicial.
Se

, então saímos do conjunto dos Reais.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Irracional
por luanxd » Ter Fev 09, 2010 23:44
- 2 Respostas
- 2078 Exibições
- Última mensagem por MarceloFantini

Qua Fev 10, 2010 12:38
Sistemas de Equações
-
- equação irracional
por Rosana Vieira » Ter Nov 29, 2011 13:51
- 1 Respostas
- 1608 Exibições
- Última mensagem por ivanfx

Ter Nov 29, 2011 15:04
Funções
-
- Equação irracional
por PeterHiggs » Sex Set 28, 2012 12:33
- 2 Respostas
- 1564 Exibições
- Última mensagem por PeterHiggs

Sex Set 28, 2012 22:14
Álgebra Elementar
-
- Equação irracional
por Flordelis25 » Sáb Abr 20, 2013 17:39
- 2 Respostas
- 1580 Exibições
- Última mensagem por Flordelis25

Sex Mai 24, 2013 17:17
Equações
-
- Equaçao Irracional
por Amanda91 » Qua Jul 10, 2013 03:05
- 3 Respostas
- 1829 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 02, 2013 09:14
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0 1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0](/latexrender/pictures/ad45e81e28805e8c29af8efdbf2dcfcd.png)

![1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0 1=x-\sqrt[]{x^2-11}\Rightarrow (1-x)^2=(-\sqrt[]{x^2-11})^2\Rightarrow 1-2x+x^2=-(x^2-11)\Rightarrow 1-2x+x^2=-x^2 +11\Rightarrow -2x^2-2x-10=0](/latexrender/pictures/ad45e81e28805e8c29af8efdbf2dcfcd.png)

![{(-\sqrt[]{{x}^{2}-11})}^{2} = \left|{x}^{2}-11 \right| {(-\sqrt[]{{x}^{2}-11})}^{2} = \left|{x}^{2}-11 \right|](/latexrender/pictures/43fa8852cb028aa21e21d3eed107c182.png) .
.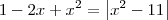 .
. , isto é,
, isto é,![x>\sqrt[]{11}\simeq3,3166 x>\sqrt[]{11}\simeq3,3166](/latexrender/pictures/fdd1826941c4141b5776552083be6382.png) então temos a equação
então temos a equação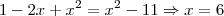
 , então saímos do conjunto dos Reais.
, então saímos do conjunto dos Reais.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.