por Luiz Felipe » Ter Jun 05, 2012 21:32
Questão : Um marceneiro cortou uma tabua retangular de 75 cm de comprimento por 20 cm de largura , separando-a em dois trapezios congruentes.Sabendo-se que o comprimento do corte foi de 25 cm, calcule a medida da base menor de um dos trapézios.
- FIGURA
- edaasaas.JPG (3.7 KiB) Exibido 2710 vezes
RESP: 30CMTentativa : eu peguei a base menor do trapezio e formei um triângulo retangulo, (largura-cateto oposto 20cm, corte-hipotenusa 25cm, base menor "x"), tentei usa um Pitagoras, mas não bateu com a resposta, segue a resolução :
![{a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15](/latexrender/pictures/749f99f2c20ad8724eb0f59b9b45935b.png "{a}^{2}={b}^{2}+{c}^{2}
{25}^{2}={20}^{2}+{x}^{2}
625 = 400 + {x}^{2}
{x}^{2}=225
x = \sqrt[2]{225}
x =15")
Agradeço a atenção, o tempo e a ajuda de quem se dispor, obrigado.
-
Luiz Felipe
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Seg Fev 13, 2012 15:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciências Biologicas
- Andamento: cursando
por MarceloFantini » Qua Jun 06, 2012 02:28
Sua resolução está incompleta. Veja a figura anexada para entender melhor. O que você fez foi encontrar o tamanho do cateto restante. Agora, sabemos que tudo vale 15, logo este pedaço debaixo vale
. Como temos um retângulo, o lado de cima é igual ao lado debaixo, daí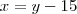
, e também sabemos
. Isolando
em função de
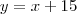, segue
e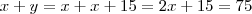
, finalmente
.
- Anexos
-
- Desenho auxiliar
- geometria.png (3.3 KiB) Exibido 2706 vezes
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por Pandaludo » Ter Ago 06, 2013 17:31
Professor, MarceloFantini , por que o senhor disse que aqueles lados eram iguais, se no texto isto não estava explícito? Refiro-me ao x. Obrigada.
-
Pandaludo
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Ter Ago 06, 2013 17:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em geometria plana
por tadeutato » Seg Abr 25, 2011 11:26
- 2 Respostas
- 1559 Exibições
- Última mensagem por SidneySantos
Seg Abr 25, 2011 22:33
Geometria Plana
-
- Duvida - Geometria Plana 2
por Luiz Felipe » Ter Jun 05, 2012 22:27
- 1 Respostas
- 1060 Exibições
- Última mensagem por MarceloFantini
Qua Jun 06, 2012 02:38
Geometria Plana
-
- Duvida - Geometria Plana 3
por Luiz Felipe » Ter Jun 05, 2012 22:48
- 1 Respostas
- 7762 Exibições
- Última mensagem por MarceloFantini
Qua Jun 06, 2012 02:45
Geometria Plana
-
- [Geometria Plana] Duvida
por Micael » Qui Mar 14, 2013 17:57
- 1 Respostas
- 1030 Exibições
- Última mensagem por timoteo
Qui Mar 14, 2013 18:34
Geometria Plana
-
- [Geometria Plana] DÚVIDA
por Micael » Seg Mai 13, 2013 19:38
- 1 Respostas
- 2600 Exibições
- Última mensagem por Molina
Seg Mai 13, 2013 23:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
