 por nandabhz » Dom Jun 03, 2012 16:48
por nandabhz » Dom Jun 03, 2012 16:48
To em duvida nestas 3 questoes de estatisticas abaixo. Alguem poderia me ajudar a resolver? Já coloquei as respostas, porem nao consegui desenvolve-las. Desde já agradeço.
1- As vendas diárias de uma lanchonete seguem uma distribuição normal, com média de R$400,00 e desvio padrão igual a R$ 100,00. Calcule a probabilidade de que em um determinado dia o faturamento da lanchonete esteja entre R$ 380,00 e R$500,00. Resposta 42,06
2-Uma grande revista de negócios brasileira afirmou que o faturamento das indústrias de uma determinada região do país seria igual a R$820.000,00. Sabe-se que o desvio padrão populacional de todas as empresas desta região é igual a R$120.000,00. Um pesquisador independente analisou os dados de uma amostra formada por 19 empresas desta região, encontrando um faturamento médio de R$750.000,00. Assumindo nível confiança de 95% (Ztab=±1,96), é possível concordar com a alegação feita pela revista? Resposta: Como Ztab= ± 1,96 (95% deconfiança), o valor de Zcalc= -2,54 não pertence ao intervalo da Ho (-1,96<zcalc < 1,96), portanto está localizado na região de rejeição (RR) que indica a
hipótese nula (Ho) deve ser rejeitada e, assim deverá ser aceita a H1 (? ? R$820.000,00). Assim é possível supor com base nas informações da amostra que a alegação feita pela revista não seja verdadeira.
3-Uma empresa que comercializa banco de dados com informações sobre assinantes de jornais e revistas assegura que a renda média dos assinantes é de, no mínimo, R$850,00. Uma amostra aleatória com 24 pessoas revelou uma média mensal igual à R$ 800,00, com desvio padrão amostral de R$200,00. Estatisticamente é possível concordar com a alegação da empresa? Assuma um nível de confiança de 95%.( dado: ztab = 1,96). Resposta Resposta: tcalc=-1,22, Como ttab= ± 2,064 (95% de confiança – Tabela ANEXO; n-1=23), o valor de tcalc= - 1,22, está localizado está no intervalo delimitado pelos valores tabelados (-2,064< tcalc<+2,064) ,ou seja, está localizado na região de aceitação de Ho indicando que a renda média dos assinantes é de, no mínimo, R$850,00.


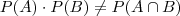
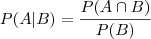
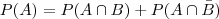
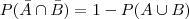


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)