 por alicemneves » Seg Mai 28, 2012 00:20
por alicemneves » Seg Mai 28, 2012 00:20
Suponha que a diminuição na pressão sanguínea de uma pessoa dependa de uma determinada droga que ela deverá tomar. Assim, se x mg da droga forem tomados, a queda na pressão sanguínea será uma função de x. Seja f(x) esta função:
f (x) = 1/2 x² (k - x)
onde x está em [0, k] e k é uma constante positiva; Determine o valor de x que cause o maior decréscimo na pressão sanguínea.
Resolução:
Para resolver este problema, sei que o ponto máximo da função deve ser encontrado, para isso devemos derivar essa função e depois igualar à zero.
Mas não estou conseguindo fazer a derivada!
-
alicemneves
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 27, 2012 23:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: cursando
 por LuizAquino » Seg Mai 28, 2012 18:05
por LuizAquino » Seg Mai 28, 2012 18:05
alicemneves escreveu:Suponha que a diminuição na pressão sanguínea de uma pessoa dependa de uma determinada droga que ela deverá tomar. Assim, se x mg da droga forem tomados, a queda na pressão sanguínea será uma função de x. Seja f(x) esta função:
f (x) = 1/2 x² (k - x)
onde x está em [0, k] e k é uma constante positiva; Determine o valor de x que cause o maior decréscimo na pressão sanguínea.
alicemneves escreveu:Resolução:
Para resolver este problema, sei que o ponto máximo da função deve ser encontrado, para isso devemos derivar essa função e depois igualar à zero.
Ok.
alicemneves escreveu:Mas não estou conseguindo fazer a derivada!
Qual foi exatamente a sua dúvida no cálculo da derivada? Por favor, envie sua tentativa para que possamos corrigi-la.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por alicemneves » Seg Mai 28, 2012 19:03
por alicemneves » Seg Mai 28, 2012 19:03
Acho que deve ser usada a regra do produto, certo?
Mas não tenho ideia de como calcular a derivada de (k -x)
-
alicemneves
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 27, 2012 23:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: cursando
 por Russman » Seg Mai 28, 2012 19:11
por Russman » Seg Mai 28, 2012 19:11
alicemneves escreveu:
f (x) = 1/2 x² (k - x)
Não entendo como que os termos se relacionam nessa função. A função é 1 sobre o produto x²(k-x)? Ou um meio que multiplica o produto...? Ou...
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por alicemneves » Seg Mai 28, 2012 19:17
por alicemneves » Seg Mai 28, 2012 19:17
A função é um meio de x², multiplicado por (k-x)
-
alicemneves
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 27, 2012 23:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: cursando
 por Russman » Seg Mai 28, 2012 20:42
por Russman » Seg Mai 28, 2012 20:42
Eu vejo duas formas de fazer: regra do produto ou expansão.
Eu sugiro a expansão! Veja, que a sua função
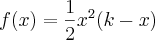
pode ser escrita como

Assim, sua derivada é
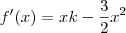
que se anula em

ou
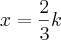
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por alicemneves » Qui Mai 31, 2012 12:07
por alicemneves » Qui Mai 31, 2012 12:07
Consegui calcular
Mas como você chegou nestes valores de x?
-
alicemneves
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 27, 2012 23:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: cursando
 por Russman » Qui Mai 31, 2012 22:58
por Russman » Qui Mai 31, 2012 22:58
É só calcular as raízes da equação!

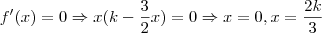
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2007 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida] Integral e ponto máximo de uma função
por ruisu » Seg Mar 04, 2013 15:19
- 1 Respostas
- 1577 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:14
Cálculo: Limites, Derivadas e Integrais
-
- Pontos maximo e minimos de uma funçao e ponto de sela
por b11adriano » Sáb Out 04, 2014 14:56
- 2 Respostas
- 2823 Exibições
- Última mensagem por Marcos Ueder

Qui Set 17, 2015 18:09
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Máximo
por Ana_Bela » Qui Nov 27, 2014 11:08
- 1 Respostas
- 1373 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 11:46
Funções
-
- Derivada através de Ponto Máximo - Otimização
por Suriano » Qua Mai 06, 2009 20:42
- 3 Respostas
- 6214 Exibições
- Última mensagem por Suriano

Qua Mai 13, 2009 21:39
Cálculo
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




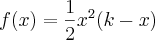

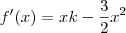
 ou
ou 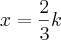 .
.
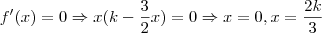 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

