 por iceman » Dom Mai 27, 2012 18:43
por iceman » Dom Mai 27, 2012 18:43
Bom, eu não sei exatamente se é números complexos, aí vai a questão:
Determinar as raízes da equação
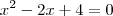
Eu fiz assim:
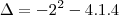
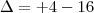

Como -12 é menor que zero a raíz fica -1 Certo?
Como faço para determinar a outra raíz? Agora eu não sei.
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 18:49
por DanielFerreira » Dom Mai 27, 2012 18:49
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por iceman » Dom Mai 27, 2012 19:00
por iceman » Dom Mai 27, 2012 19:00
Fica
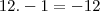
?
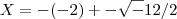
Nessa parte eu não sei pois 12 não tem raíz, fica
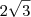
?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 20:58
por DanielFerreira » Dom Mai 27, 2012 20:58
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pessoal, poderia me ajudar nesta questão?!
por zenildo » Ter Ago 05, 2014 08:38
- 1 Respostas
- 867 Exibições
- Última mensagem por zenildo

Qua Ago 06, 2014 08:55
Geometria Plana
-
- Alguém pode corrigir?
por Giles » Sex Nov 07, 2008 09:06
- 6 Respostas
- 7372 Exibições
- Última mensagem por Giles

Sex Nov 07, 2008 19:48
Estatística
-
- Derivada direcional e gradiente(só corrigir)?
por miyasato » Qua Jun 17, 2015 13:35
- 1 Respostas
- 2723 Exibições
- Última mensagem por adauto martins

Qua Jun 17, 2015 20:41
Cálculo: Limites, Derivadas e Integrais
-
- Por favor me ajudem Questão deN° de habitantes
por Rodrigopc1 » Seg Out 19, 2009 22:31
- 1 Respostas
- 2835 Exibições
- Última mensagem por Rodrigopc1

Seg Out 19, 2009 22:33
Sistemas de Equações
-
- Ajuda, por favor, em uma questão da UFES
por rah_marques » Qua Out 21, 2009 18:08
- 0 Respostas
- 1638 Exibições
- Última mensagem por rah_marques

Qua Out 21, 2009 18:08
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
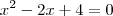
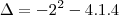
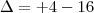


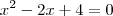
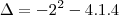
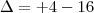


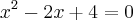
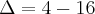
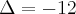

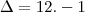
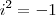
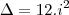
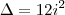
![x' = \frac{- b + \sqrt[]{\Delta}}{2a} x' = \frac{- b + \sqrt[]{\Delta}}{2a}](/latexrender/pictures/f4d6d44574cf14cc09038001344510a4.png)
![x' = \frac{- b - \sqrt[]{\Delta}}{2a} x' = \frac{- b - \sqrt[]{\Delta}}{2a}](/latexrender/pictures/a8d1e25722daecfcd32e02994e8a7ada.png)

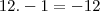 ?
?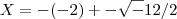 Nessa parte eu não sei pois 12 não tem raíz, fica
Nessa parte eu não sei pois 12 não tem raíz, fica 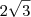 ?
?
![x' = \frac{- ( - 2) + \sqrt[]{12i^2}}{2.1} x' = \frac{- ( - 2) + \sqrt[]{12i^2}}{2.1}](/latexrender/pictures/66c5e98d090c53a7dc54c4fc61869cf6.png)
![x' = \frac{2 + \sqrt[]{4.3i^2}}{2} x' = \frac{2 + \sqrt[]{4.3i^2}}{2}](/latexrender/pictures/8b78a1933471ad3b33cbc60cde53aa04.png)
![x' = \frac{2 + 2i\sqrt[]{3}}{2} x' = \frac{2 + 2i\sqrt[]{3}}{2}](/latexrender/pictures/7b71f82f9a6c5ee0df4618d371e94b27.png)
![x' = 1 + i\sqrt[]{3} x' = 1 + i\sqrt[]{3}](/latexrender/pictures/d32f35193fa6e100a668502be0788820.png)
![x'' = \frac{- ( - 2) + \sqrt[]{12i^2}}{2.1} x'' = \frac{- ( - 2) + \sqrt[]{12i^2}}{2.1}](/latexrender/pictures/d8c0356ea42832cda5bddd15ce7faa3f.png)
![x'' = \frac{2 - \sqrt[]{4.3i^2}}{2} x'' = \frac{2 - \sqrt[]{4.3i^2}}{2}](/latexrender/pictures/b9fc17a88c3e3f0fb59770334914faa8.png)
![x'' = \frac{2 - 2i\sqrt[]{3}}{2} x'' = \frac{2 - 2i\sqrt[]{3}}{2}](/latexrender/pictures/370b0aceff05d68dc74ebd915a9f7ac5.png)
![x'' = 1 - i\sqrt[]{3} x'' = 1 - i\sqrt[]{3}](/latexrender/pictures/ba9a410762165f3d5cee1408ab56c135.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.