 por iceman » Dom Mai 27, 2012 18:08
por iceman » Dom Mai 27, 2012 18:08
Oi, eu aqui denovo, peço ajuda para essa questão:
Dado o número complexo
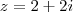
Calcular

a)

b)
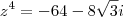
c)

d)

e) Nenhuma das alternativas
Obrigado quem me ajudar =D
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 18:21
por DanielFerreira » Dom Mai 27, 2012 18:21
Dica:
calcule

depois faça
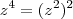
.
Lembre-se que:


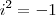
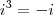
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por iceman » Dom Mai 27, 2012 19:12
por iceman » Dom Mai 27, 2012 19:12
danjr5 escreveu:Dica:
calcule

depois faça
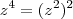
.
Lembre-se que:


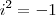
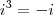

Não consigo resolver, ajuda mais ?

-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mai 27, 2012 19:17
por Russman » Dom Mai 27, 2012 19:17
Use a identidade
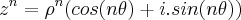
,
onde

,
![\rho=\sqrt[]{{a}^{2}+{b}^{2}} \rho=\sqrt[]{{a}^{2}+{b}^{2}}](/latexrender/pictures/209b7592ae5bb798c84e06be7af1301e.png)
e

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por iceman » Dom Mai 27, 2012 19:20
por iceman » Dom Mai 27, 2012 19:20
Russman escreveu:Use a identidade
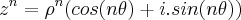
,
onde

,
![\rho=\sqrt[]{{a}^{2}+{b}^{2}} \rho=\sqrt[]{{a}^{2}+{b}^{2}}](/latexrender/pictures/209b7592ae5bb798c84e06be7af1301e.png)
e

.
Entendi nada :S Tem como resolver ai pra mim ?
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mai 27, 2012 19:32
por Russman » Dom Mai 27, 2012 19:32
Ok, esquece a identidade! k
Veja que

. Assim, como

,
então

.
Agora,
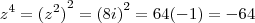
.
Editado pela última vez por
Russman em Dom Mai 27, 2012 19:38, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por iceman » Dom Mai 27, 2012 19:37
por iceman » Dom Mai 27, 2012 19:37
Russman escreveu:Ok, esquece a identidade! k
Veja que

. Assim, como

,
então

.
Agora,

.
Só uma coisa, porquê colocou sinal negativo aqui

? Obrigado por me ajudar

-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mai 27, 2012 19:38
por Russman » Dom Mai 27, 2012 19:38
Porque
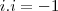
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por iceman » Dom Mai 27, 2012 19:39
por iceman » Dom Mai 27, 2012 19:39
iceman escreveu:Russman escreveu:Ok, esquece a identidade! k
Veja que

. Assim, como

,
então

.
Agora,

.
Só uma coisa, porquê colocou sinal negativo aqui

? Obrigado por me ajudar

AAAAh desculpa te incomodar, mais porquê aqui ficou assim:

? Obrigado mais uma vez D;
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Dom Mai 27, 2012 19:43
por Russman » Dom Mai 27, 2012 19:43
Tem que calcular
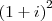
.
Isso é

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por iceman » Dom Mai 27, 2012 21:01
por iceman » Dom Mai 27, 2012 21:01
iceman escreveu:Russman escreveu:Ok, esquece a identidade! k
Veja que

. Assim, como

,
então

.
Agora,

.
Só uma coisa, porquê colocou sinal negativo aqui

? Obrigado por me ajudar

Ainda não entendi o jogo de sinal nessa parte aqui:

( o -1 que eu não consigo entender.) Help ? D;
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 21:07
por DanielFerreira » Dom Mai 27, 2012 21:07
Russman escreveu:Porque
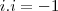
.
ou
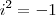
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por iceman » Dom Mai 27, 2012 21:12
por iceman » Dom Mai 27, 2012 21:12
danjr5 escreveu:Russman escreveu:Porque
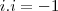
.
ou
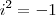
Valeuuuuuuuu

-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 21:26
por DanielFerreira » Dom Mai 27, 2012 21:26
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão - números complexos
por Danilo » Sex Ago 03, 2012 02:27
- 1 Respostas
- 2062 Exibições
- Última mensagem por e8group

Sex Ago 03, 2012 11:15
Números Complexos
-
- Questão - Números Complexos
por Glauber_Garcia » Qua Nov 28, 2012 21:25
- 2 Respostas
- 4785 Exibições
- Última mensagem por Direito

Qua Mar 13, 2013 01:15
Números Complexos
-
- [números complexos] questão unicentro
por Flavia R » Qui Ago 25, 2011 11:39
- 4 Respostas
- 3562 Exibições
- Última mensagem por Flavia R

Qui Ago 25, 2011 21:23
Números Complexos
-
- [Números complexos] Dúvida em questão
por iceman » Qui Mai 10, 2012 18:46
- 3 Respostas
- 2756 Exibições
- Última mensagem por fraol

Qui Mai 10, 2012 19:41
Números Complexos
-
- [Números Complexos] Questão envolvendo Potenciação
por everton_stark » Sáb Dez 26, 2015 22:49
- 1 Respostas
- 8730 Exibições
- Última mensagem por rzarour

Sex Abr 01, 2016 07:18
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
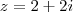 Calcular
Calcular 

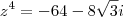



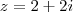 Calcular
Calcular 

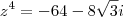



 depois faça
depois faça 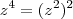 .
.

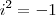
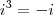

depois faça
.



,
,
e
.

 . Assim, como
. Assim, como ,
, .
.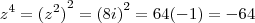 .
.
. Assim, como
,
.
.
 ? Obrigado por me ajudar
? Obrigado por me ajudar 


. Assim, como
,
.
.
? Obrigado por me ajudar
 ? Obrigado mais uma vez D;
? Obrigado mais uma vez D;

. Assim, como
,
.
.
? Obrigado por me ajudar
 ( o -1 que eu não consigo entender.) Help ? D;
( o -1 que eu não consigo entender.) Help ? D;
.
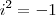

.





![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.